

• L'oscillateur
électrique est constitué, d'un amplificateur non
inverseur bâti autour d'un amplificateur opérationnel muni
des résistances R1 et R2 assurant une
réaction négative ; et d'un réseau
déphaseur
(le pont de WIEN)
constitué par la mise en série, d'un
dipôle série R0, C0, et d'un
dipôle parallèle R0, C0.
• On fait l'hypothèse
que l'amplificateur opérationnel est quasiment idéal, il
n'absorbe aucun courant sur ses entrées différentielles,
sont gain différentiel est "très grand"...
• Le réseau
déphaseur soumis au potentiel de sortie `v_s(t)` de
l'amplificateur non inverseur, alimente sous le potentiel `v_r(t)`
l'entrée de ce même amplificateur ; on dit alors que l'on
a
affaire à un système bouclé.
• Pour une fréquence
`f_n` caractéristique du réseau déphaseur, le
potentiel `v_r(t)` est en phase avec le potentiel `v_s(t)` .
• Dans ces conditions, le
potentiel `v_r(t)`, image du potentiel `v_s(t)`, est amplifié
par l'amplificateur non inverseur, qui pour un réglage
convenable des résistances R1 et R2
compense l'atténuation apportée par le réseau
déphaseur.
• Ainsi peut-on (ici)
créer et entretenir des oscillations électriques dont on
maîtrise a priori la fréquence.
• On se place dans le
cadre
du fonctionnement décrit au paragraphe 1.3..
• On retient donc
l'hypothèse du régime harmonique et on suppose que le
système fonctionne en régime linéaire.
• On suppose
également que l'amplificateur opérationnel a un
comportement quasiment idéal.
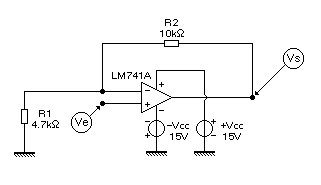
• On suppose ici que
l'amplificateur est soumis à un signal d'entrée `v_e(t)`
(qui après bouclage s'identifiera à `v_r(t)`).
• Compte tenu des
hypothèses du paragraphe
2.1.,
on peut
écrire :
`ul(V_s)=(1+R_2/R_1)ul(V_e)`, où
`ul(V_s)`et `ul(V_e)`sont les représentants complexes des
potentiels `v_s(t)`et `v_e(t)`, qui sont donc a priori, des
fonctions sinusoïdales du temps.
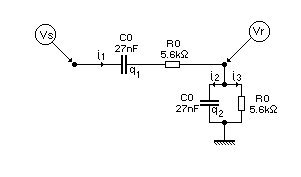
• Ce réseau
déphaseur constitue ce que l'on appelle un pont de WIEN.
• On peut écrire :
`ul(V_r)=ul(V_s)/(1+(R_0+1/(jC_0 omega)).(1/R_0+jC_0 omega))` .
- Où : `ul(V_r)`et `ul(V_s)`sont les représentants
complexes des
potentiels `v_r(t)`et `v_s(t)`, qui sont a priori, des
fonctions sinusoïdales du temps.
- La quantité : `R_0+1/(jC_0 omega)`
représente l'impédance complexe du circuit série R0,
C0 .
- La quantité : `1/R_0+jC_0 omega` représente
l'admittance complexe du circuit parallèle R0, C0
.
• Un développement
élémentaire conduit à : `ul(V_r)=(jR_0C_0 omega
ul(V_s))/(1-R_0^2C_0^2 omega^2+j3R_0C_0 omega)`.
- On pose : `omega_n=1/(R_0 C_0) hArr f_n=1/(2piR_0C_0)`, alors il
vient : `ul(V_r)=(jf/f_n .ul(V_s))/(1-(f/f_n)^2+j3f/f_n)`.
- On observe que pour `f=f_n`, `ul(V_r)=ul(V_s)/3`.
- Alors `v_r(t)` et `v_s(t)`sont en phase, cependant l'amplitude Vr
de `v_r(t)` n'est plus que le tiers de l'amplitude Vs de
`vs(t)` .
Note : Ici `f_n~~1
kHz`.
• Des oscillations
électriques à la fréquence `f_n` peuvent
apparaître au sein du circuit bouclé, à condition
que l'amplificateur ait un gain égal (ici) au minimum à
trois,
pour compenser l'atténuation apportée par le
réseau déphaseur.
• On doit alors
vérifier : `3<=(1+R_2/R_1) rArr 2R_1<=R_2`.
Note : Si
`R_1=4,7 kOmega`, alors il faut choisir `9,4
kOmega<=R_2`, et dans la série E12, on choisira :
`R_2=10
kOmega`.
• Nous venons de retrouver
les conditions dites de BARKHAUSEN.

Remarque
: Ce graphe a été tracé à l'aide du
logiciel gnuplot®.
• Sur la base des
résultats précédents, on câble la structure
et l'on obtient bien les oscillations prévues ; cependant nous
ne sommes pas maître de l'amplitude des oscillations, et on
observe même que le signal de sortie est quelque peu
écrêté à la valeur des potentiels de
saturation `+-V_(sat)` de l'amplificateur opérationnel.
• La fréquence
d'oscillation est proche de 1 kHz.
• L'approche intuitive
précédente, décrit de manière imparfaite le
fonctionnement du montage ; ainsi sommes nous incapables de
prédire l'amplitude des oscillations `v_s(t)` et `v_r(t)`.
• Aussi dans les paragraphes
qui suivent, allons nous prendre en compte une non
linéarité qui apparaît lors du fonctionnement du
montage et qui permet de décrire de manière intelligible
son fonctionnement.
• À l'évidence c'est l'amplificateur non inverseur qui est à l'origine d'une non linéarité que nous allons modéliser sous la forme d'une saturation.
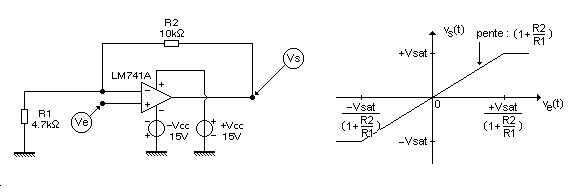
Note : Nous
faisons toujours l'hypothèse que l'amplificateur
opérationnel a un comportement idéal, et les potentiels
de saturation supposés symétriques sont notés
`+-V_(sat)`.
• Tant que :
`|v_e(t)|<V_(sat)/(1+R_2/R_1)` , l'amplificateur non inverseur a un
comportement linéaire, et on peut écrire :
`v_s(t)=(1+R_2/R_1)v_e(t)` .
• Dès que :
`V_(sat)/(1+R_2/R_1)<=|v_e(t)|` , l'amplificateur non inverseur est
saturé et `v_s(t) = +-V_(sat)` , du signe de `v_e(t)`.

• À chaque instant
on
peut écrire : `i_1=i_2+i_3` , `i_3=v_r/R_0` , `q_1=C_0(v_s
-R_0.i_1-v_r)` , `i_1=(dq_1)/(dt)` , et `i_2=C_0 (dv_r)/(dt)` .
• Un développement
élémentaire conduit à l'équation
différentielle suivante :
`R_0^2C_0^2(d^2v_r)/(dt^2)+3R_0C_0(dv_r)/(dt)+v_r=R_0C_0(dv_s)/(dt)` .
• Comme le système est maintenant bouclé, `v_e(t)` s'identifie à `v_r(t)`.
• Alors
: `|v_r(t)|<V_(sat)/(1+R_2/R_1)` ; d'où
`v_s(t)=(1+R_2/R_1)v_r(t)` , et
`(dv_s(t))/(dt)=(1+R_2/R_1)(dv_r(t))/(dt)` .
• On a donc une
équation de contrainte liant `v_s(t)` à `v_r(t)` ; aussi
l'équation différentielle développée au
paragraphe 3.2.
s'écrit-elle :
`R_0^2C_0^2(d^2v_r)/(dt^2)+3R_0C_0(dv_r)/(dt)+v_r=R_0C_0(1+R_2/R_1)(dv_r(t))/(dt)`
.
- Soit encore :
`R_0^2C_0^2(d^2v_r)/(dt^2)+R_0C_0(3-(1+R_2/R_1))(dv_r)/(dt)+v_r=0` .
- Ou plus simplement :
`R_0^2C_0^2(d^2v_r)/(dt^2)+R_0C_0(2-R_2/R_1)(dv_r)/(dt)+v_r=0`.
• Alors
: `V_(sat)/(1+R_2/R_1)<=|v_r(t)|` ; d'où
`v_s(t)=+-V_(sat)` , du signe de `v_r(t)`, et
`(dv_s(t))/(dt)=0` .
• On a donc une nouvelle
équation de contrainte liant `v_s(t)` à `v_r(t)` ; aussi
l'équation différentielle développée au
paragraphe 3.2.
s'écrit-elle maintenant :
`R_0^2C_0^2(d^2v_r)/(dt^2)+3R_0C_0(dv_r)/(dt)+v_r=0`
.
• Suivant les usages...
nous
allons mettre les équations sous forme canonique, c'est à
dire :
`1/omega_n^2 (d^2v_r)/(dt^2)+2 z/omega_n (dv_r)/(dt)+v_r=0` .
- Où `omega_n` désigne la pulsation naturelle du
système physique (`f_n=omega_n/(2pi)` en est la fréquence
naturelle) , et où `z` désigne le facteur d'amortissement
du système physique.
• Pour
: `|v_r(t)|<V_(sat)/(1+R_2/R_1)` , on est en régime
linéaire, et on écrit :
`1/omega_n^2 (d^2v_r)/(dt^2)+2 z_L/omega_n (dv_r)/(dt)+v_r=0` .
- Avec : `omega_n=1/(R_0C_0)` , `f_n=1/(2piR_0C_0)` , et
`z_L=1-R_2/(2R_1)` .
• Pour
: `V_(sat)/(1+R_2/R_1)<=|v_r(t)|` , on est en régime non
linéaire, et on écrit :
`1/omega_n^2 (d^2v_r)/(dt^2)+2 z_(NL)/omega_n (dv_r)/(dt)+v_r=0` .
- Avec une fois encore : `omega_n=1/(R_0C_0)` ,
`f_n=1/(2piR_0C_0)` , et `z_(NL)=3/2` .
• Avec R0 =
5,6
kΩ et C0 = 27
nF, il vient: `f_n~~1 kHz`.
• Pour le régime
linéaire, avec R2 = 10 kΩ et R1
=
4,7 kΩ, il vient: `z_L~~-0,064` ; alors `z_L < 0` .
- Aussi les racines de l'équation caractéristique :
`p^2/omega_n^2+2z_L p/omega_n+1=0`, sont-elles égales à :
`p_(1//2)=-omega_n z_L +- j omega_n sqrt(1-z_L^2`.
- Comme `z_L < 0` , ces racines sont à partie réelle
positive `(-omega_n z_L)` , cela conduit à une solution
fonction sinusoïdale du temps (présence du terme `j
omega_n sqrt(1-z_L^2` ), pondérée par le facteur
`e^(-omega_n z_L t` qui
correspond à une croissance exponentielle dans le temps, ce qui entraîne
inévitablement le dispositif vers une saturation !
• Pour le régime
non linéaire, `z_(NL)=1,5` ; alors `0<z_(NL)` .
- Aussi les racines de l'équation caractéristique :
`p^2/omega_n^2+2z_(NL) p/omega_n+1=0`, sont-elles égales
à :
`p_(1//2)=-omega_n z_(NL) +- omega_n sqrt(z_(NL)^2-1)`.
- Comme `0<z_(NL)` , ces racines sont réelles et
négatives, ce qui conduit à une solution
contenant des exponentielles qui décroissent dans le temps, ce
qui entraîne
a priori le dispositif vers l'état de repos !
• Il est clair que la
discussion relative à la description des oscillations
électriques ne peut plus aller plus avant ; aussi "faut-il
passer" à l'intégration des équations ; c'est ce
que nous allons décrire dans les paragraphes qui suivent, en
mettant en oeuvre une méthode d'intégration
numérique, la méthode de RUNGE-KUTTA
d'ordre quatre
(RK4,4) .
• La méthode
de
RUNGE-KUTTA RK4,4
est une méthode numérique permettant de résoudre
dans le cas le plus général, un système
d'équations différentielles ordinaires (EDO) du premier
ordre par approximation. Cette méthode a été mise
au point par les mathématiciens Carl
RUNGE et Martin Wilhelm KUTTA.
- Rappelons qu'une équation différentielle
ordinaire (EDO) de degré n, est de la forme :
`F(x,y(x),doty(x),ddoty(x),...,y^((n)) (x))=0`, où `y^((n)) (x)`
est la derivée n-ième de `y(x)` par rapport à `x`.
- Pour une équation différentielle
ordinaire du premier ordre, on calcule la solution de l'équation
différentielle par itération, le raffinement de la
méthode conduit à une erreur d'ordre quatre.
- Lorsque l'on a affaire à une
équation différentelle ordinaire d'ordre n
supérieur ou égal à deux, on peut la
décomposer en un système
de n équations
différentielles ordinaires du premier ordre. On constitue alors
un espace vectoriel des solutions, de dimension fini ; on dit que
l'équation différentielle ordinaire de degré n est une
fonction à valeur vectorielle. Bien entendu, la méthode
de RUNGE-KUTTA RK4,4
s'applique à chaque composante vectorielle.
• Partons de l'expression
générale de l'équation de fonctionnement :
`1/omega_n^2 (d^2v_r)/(dt^2)+2 z/omega_n (dv_r)/(dt)+v_r=0` , où
`z` peut prendre la valeur `z_L` ou `z_(NL)` ; aussi l'équation
n'est-elle pas à coefficients constants ! Il y a une non
linéarité...
• Nous pouvons écrire
l'équation sous la forme : `1/omega_n^2 ddotv_r+2 z/omega_n
dotv_r+v_r=0` .
- Où : `dotv_r=(dv_r)/(dt)` et `ddotv_r=(d dotv_r)/(dt)` .
- On peut encore écrire : `ddotv_r=-omega_n(omega_n v_r+2z
dotv_r)` .
• Nous allons
décomposer cette équation différentielle ordinaire
du second ordre, en un système de deux équations
différentielles ordinaires du premier ordre.
• Posons : `ul(v_r=u_0)`, et
`(du_0)/(dt)=u_1` ; on en déduit `u_1=(dv_r)/(dt)`, soit
`ul(dotv_r=u_1)` et `(du_1)/(dt)=(d dotv_r)/(dt)`, soit
`ul(ddotv_r=(du_1)/(dt))`.
•
L'équation s'écrit alors : `(du_1)/(dt)=-omega_n(omega_n
u_0+2z u_1)` .
• Nous devons
donc résoudre le systèmes de deux équations
différentielles ordinaires du premier ordre suivant :
`color(navy)((du_0)/(dt)=u_1)`
`color(navy)((du_1)/(dt)=-omega_n(omega_n u_0+2z u_1))`
• Où :
`u_0=u_0(t)` et `u_1=u_1(t)` sont des fonctions du temps `t`.
Remarque : On a
affaire à un système d'équations couplées,
où
`z` peut prendre la valeur `z_L` ou `z_(NL)` !
• Dans la
méthode de RUNGE-KUTTA
RK4,4, on programme le système des
deux équations différentielles ordinaires du premier
ordre, et on précise les conditions initiales (ici au nombre
de deux).
• À
la date `t=0 s` ,` v_r(0)=0 V rArr u_0(0)=0` , et
`(dv_r(0))/(dt)=50` µV/µs ` rArr u_1(0)=50` .
Remarque : On fait
l'hypothèse que le "bruit de fond" fait fluctuer le potentiel
`color(navy) (v_r(t))` ...
• `t` prend ses
valeurs dans l'intervalle `[0, t_(Max)]`, et varie au pas `Delta t`.
• On prendra en
compte que :
- Si : `|v_r(t)|<V_(sat)/(1+R_2/R_1) rArr z=z_L` .
- Si : `V_(sat)/(1+R_2/R_1)<=|v_r(t)| rArr z=z_(NL)` .
• L'algorithme de
la méthode de RUNGE-KUTTA
RK4,4 élabore une "table de
données" constituée de n lignes contenant chacune le
triplet : {`t, u_0(t), u_1(t)`}.
- On résoud bien notre problème sous forme
numérique, et l'exploitation de la "table de données"
permet ici de donner l'évolution du signal `v_r(t)` .
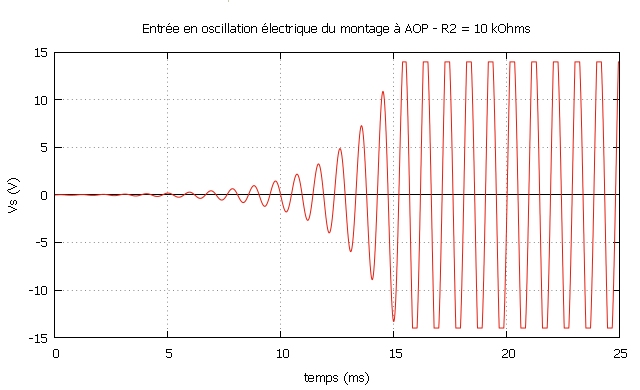
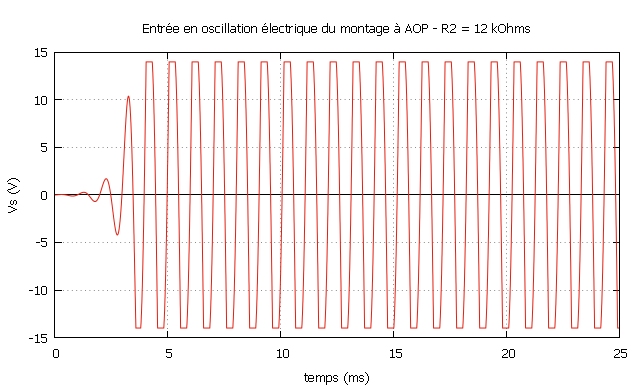
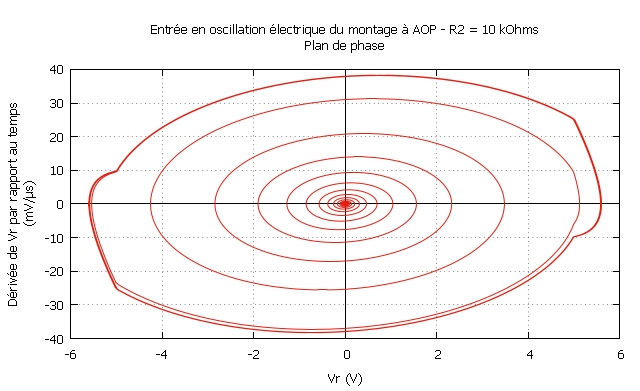
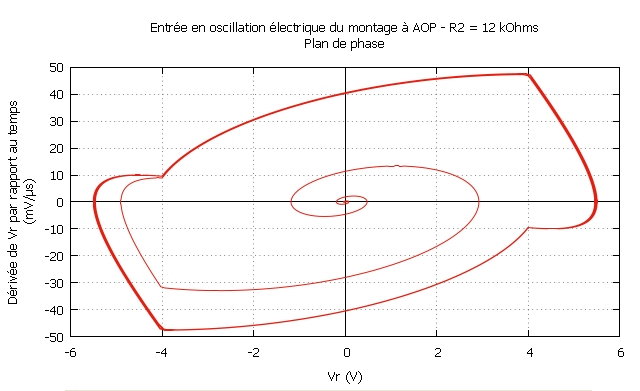
• On donne :
±Vsat = ±14 V, R0
= 5,6 kΩ, C0 = 27 nF, R1 = 4,7 kΩ, R2
= 10 kΩ ou R2 = 12 kΩ .
• Ici `t`
prend
ses
valeurs dans l'intervalle `[0, t_(Max)]`, et varie au pas `Delta t` ,
avec :
`t_(Max)=25` ms , `Delta t=25` µs.
• À
la date `t=0` s, `u_0(0)=0` , et
`u_1(0)=50` .
• Nous
obtiendrons une "table de données" formée de dix
mille lignes contenant chacune le
triplet : {`t, u_0(t), u_1(t)`}.
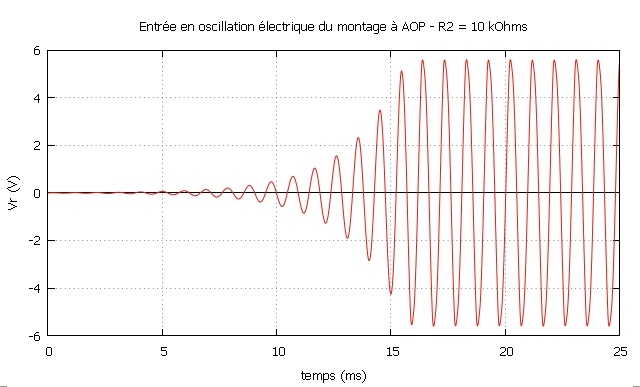
Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot®.

Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot®.
Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot®.
Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot®.
Remarque
: Ce graphe a été tracé à l'aide du
logiciel gnuplot®.
• Le signal
électrique est bien périodique, mais il n'est
certainement pas sinusoïdal !
•
L'étude
de vr(t) confirme bien l'analyse préparatoire. Sous
l'effet du
"bruit de fond", l'oscillation électrique s'amorce et
croît de manière exponentielle (en effet l'enveloppe de
vr(t) a l'allure d'une exponentielle), bientôt on
atteint
la
saturation et on passe en régime non linéaire, alors le
signal vr(t) est contraint à
décroître,
puis on passe à nouveau en régime linéaire .etc.
• Certes, on ne
maîtrise pas l'amplitude de l'oscillation électrique, et
la tension de sortie finit par être écrêtée
à `+-V_(sat)`.
• La
fréquence d'oscillation reste voisine de `f_n~~ 1 kHz`.
• A priori nous
aurions pu intégrer les équations différentielles,
mais nous aurions eu le plus grand mal à gérer le passage
du mode de fonctionnement linéaire au mode de fonctionnement non
linéaire.
• Grâce
à la méthode de RUNGE-KUTTA
RK4,4, nous accédons
aux signaux électriques "facilement".
• Cependant, nous
avons dû faire une analyse serrée, et donc "un peu de
belle
physique"...
• J'adresse mes
plus vifs remerciements à Monsieur
John BURKARDT, Chercheur invité du Département Informatique
Scientifique, Florida State University (FSU) : John
BURKARDT.
• Monsieur John
BURKARDT met à notre disposition, le code source
écrit en
C, de la méthode de RUNGE-KUTTA
RK4,4, sous le vocable rk4.c, et
un fichier d'en-tête rk4.h.
- Deux algorithmes sont développés :
• "RK4 takes one Runge-Kutta step for a scalar ODE", qui permet de
résoudre une
équation différentielle ordinaire du
premier ordre.
• "RK4VEC takes one Runge-Kutta step for a vector ODE", qui
permet de résoudre un système de n
équations
différentielles ordinaires du premier ordre, l'équation
différentielle ordinaire d'ordre n à
l'origine de ce
système de n
équations différentielles ordinaires
du premier ordre, est "bien" une fonction à valeur vectorielle.
• Monsieur John
BURKARDT met également à notre disposition, le
code
source écrit en C, de deux exemples permettant de tester les
deux algorithmes proposés, sous le vocable rk4_prb.c.
- Les trois fichiers peuvent être
téléchargés à l'URL :
<https://people.sc.fsu.edu/~jburkardt/c_src/rk4/rk4.html>.
• Pour ma part,
je vous propose de consulter un document html que j'ai
rédigé à votre intention et qui traite de la "Mise
en œuvre pratique de la méthode RK4,4 pour
l'oscillateur
à pont de WIEN", rendez-vous à la page "AOPRK4"...
• Cette page
n'aurait pas pu être composée sans les "outils" fournis
par AsciiMath, à l'URL
: <http://asciimath.org/>.
• Cette page a pu
être développée et affichée correctement
grâce à l'utilisation du réseau de distribution de
contenu MathJax (CDN). Toute
la documentation relative à MathJax
est accessible à l'URL :
<http://docs.mathjax.org/en/latest/index.html>.
• Les graphes ont
été tracés à l'aide du logiciel
gnuplot®, dont la documentation est
accessible à l'URL :
<http://www.gnuplot.info/>.
Retour à la
page principale...