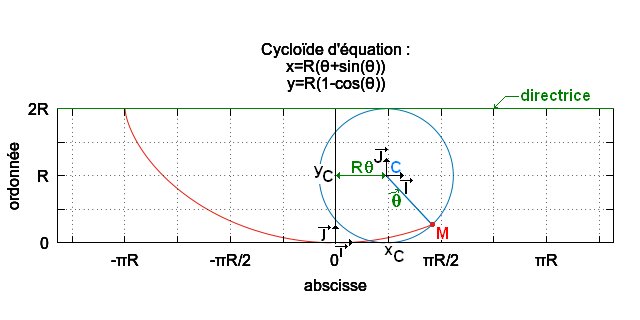
• La cycloïde droite est une courbe plane. C'est la trajectoire d'un point fixé à un cercle qui roule sans glisser sur une droite. Il s'agit ici d'une courbe cycloïdale particulière dont la directrice est une droite et dont le point directeur est situé sur le cercle lui-même.
Remarque : Figure tracée à l'aide du logiciel gnuplot®.
• Elles reprennent
les
propositions énoncées dans la définition.
• Un cercle de rayon R
délimitant un disque contenu dans le plan (Ox, Oy), roule sans
glisser "sous" une droite, la directrice
, d'équation cartésienne `y=2R AA x` .
On
étudie dans le repère (Ox, Oy) le déplacement d'un
point M
appartenant au cercle.
• Le déplacement
du point
M
dans le repère (Ox, Oy) est la combinaison du déplacemen
du
centre C
du cercle par rapport au repère (Ox, Oy) et du
déplacement du
point M
relativement au repère (`color(navy) (C), vec I, vec J`)
lié au cercle.
Remarque : Le cercle
"roule sans
glisser sous" la directrice
aussi son rayon R
tourne dans le sens direct...
• Regarder
l'animation...
• Il s'agit d'un
mouvement de rotation d'amplitude θ
autour du point C, dans le
repère (`color(navy) (C), vec I, vec J`).
• On peut
écrire : `color(navy) (vec "CM"=Rsin(theta) vec I
-Rcos(theta) vec J)`.
• Le cercle roule
sans
glisser "sous" la directrice, aussi quand le cercle tourne d'un angle
θ, le point
de contact entre le cercle et la directrice se
déplace d'une longueur égale à Rθ, le
centre du cercle effectue alors un déplacement identique.
• On peut
écrire : `color(navy) (vec "OC"=R theta vec i + R vec j)`.
• Bien entendu c'est
la
combinaison des deux déplacements précédents.
• On peut
écrire : `vec "OM"=vec "OC" + vec "CM"`.
• Soit : `vec
"OM"=R theta vec i + R vec j +
Rsin(theta) vec I
-Rcos(theta) vec J`.
• Les vecteurs : `vec i`,
`vec I`, et `vec j`, `vec J` sont équipolents.
• On peut encore
écrire : `vec "OM"=R theta vec i + R vec j +
Rsin(theta) vec i
-Rcos(theta) vec j`.
• On
peut également
écrire :
`vec "OM"=x vec i + y vec j`.
• En procédant
par identification il vient :
`color(navy) (x=R
(theta + sin(theta)))`.
`color(navy) (y=R
(1 - cos(theta)))`.
• Où le
paramètre :
`color(navy) (theta in [-pi, pi])`.
• Cette expression
différentielle s'écrit : `ds_M=sqrt(dx^2+dy^2)`.
Remarque :
Pour mettre en place la démonstration , on se place à
droite de l'origine O , alors
`theta in [0,pi]`, et on se déplace vers la droite...
• On écrit :
`dx=R(1+cos(theta))d theta`, et `dy=Rsin(theta)d theta`.
`ds_M^2=2R^2(1+cos(theta)) d theta^2`.
- Or : `1+cos(theta)=2cos^2(theta/2)`.
`ds_M^2=4R^2cos^2(theta/2)d theta^2`, soit `color(navy)
(ds_M=2Rcos(theta/2) d
theta)`.
• Écrivons :
`s_M=bar "OM"`
• On suppose que le
point M part de l'origine O pour laquelle
`theta=0 rArr x=0, y=0`, pour atteindre le point M0 pour
lequel
`theta=theta_0 rArr x_(M_0)=R
(theta_0 + sin(theta_0)), y_(M_0)=R
(1 - cos(theta_0))`.
• Il vient :
`s_(M_0)=int_(0)^(theta_0)2Rcos(theta/2)d theta`, soit
`s_(M_0)=4R[sin(theta/2)]_0^(theta_0)`, et `s_(M_0)=4Rsin(theta_0/2)`.
• Pour une position
quelconque du point M sur la cycloïde, on écrit :
`color(navy) (s_M=bar "OM")` et `color(navy) (s_M=4Rsin(theta/2))`.
• Évaluons la
longueur de la cycloïde quand on passe d'une
extémité
à l'autre.
- On passe du point `M_1` pour lequel `theta_1=-pi`, au point
`M_2` pour lequel `theta_2=pi`.
`S_(M_1 M_2)=S_(M_2)-S_(M_1)`, et `S_(M_1
M_2)=4Rsin(pi/2)-4Rsin(-pi/2)`, d'où `color(blue) (S_(M_1
M_2)=8R)`.
• Cette page
n'aurait pas pu être composée sans les "outils" fournis
par AsciiMath, à l'URL
: <http://asciimath.org/>.
• Cette page a pu
être développée et affichée correctement
grâce à l'utilisation du réseau de distribution de
contenu MathJax (CDN). Toute
la documentation relative à MathJax
est accessible à l'URL :
<http://docs.mathjax.org/en/latest/index.html>.
• Les graphes et les
animations ont
été tracés à l'aide du logiciel
gnuplot®, dont la documentation est
accessible à l'URL :
<http://www.gnuplot.info/>.
Retour à la page précédente...