• Une courbe
tautochrone est une courbe où le temps τ pris par
une masse
ponctuelle m
glissant sans frottement et sans vitesse initiale sous l'influence de
la gravité jusqu'à son point
le plus bas, est indépendant de son point de départ.
• Nous allons
démontrer que la cycloïde est une courbe tautochrone.

• Une masse
ponctuelle m
glisse sur une cycloïde, sans
frottement, sous l'influence de la gravité, entre deux points M1
et M2. Au point `M_1(x_1,y_1)` la
masse
ponctuelle a une vitesse initiale nulle, le point `M_2(0,0)` est le
point le plus bas de son parcours.
• La cycloïde a
comme représentation paramétrique :
`x=R(theta+sin(theta))`
`y=R(1-cos(theta)) hArr y=2Rsin^2(theta/2)`
- Où : `theta in [-pi,0]`.
- On rappelle que l'abscisse curviligne du point M mesurée
à partir de l'origine O est donnée par :
`s_M=4Rsin(theta/2)`.
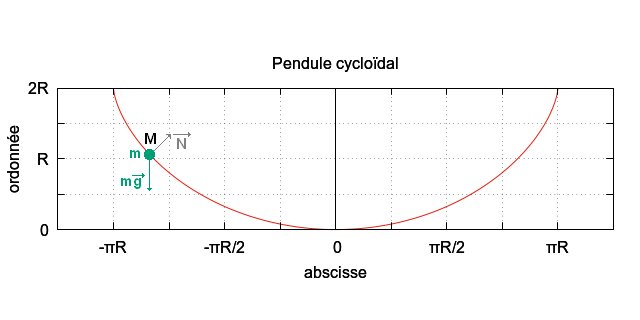
• Dans ce
système physique, seul le poids `vec P`de la masse m travaille, en
effet la réaction `vec N`du support est perpendiculaire à
son dépacement, il y a donc conservation de l'énergie
totale du système physique.
`E=1/2 mv^2 +mgy` est constante.
- En M1 la masse ponctuelle m est au repos
aussi : `E=mgy_1`
- On peut alors
écrire : `color(navy) (1/2 mv^2+mgy =mgy_1)`.
• Notons ds la distance
élémentaire parcourue par la masse m pendant le
temps élémentaire dt.
• Si nous connaissons
la vitesse
algébrique v
de la masse m
sur la cycloïde, alors : `dt=(ds)/v`.
Remarque : ds
s'identifie avec la différentielle
de l'abscisse curviligne de la masse m sur la
cycloïde.
• La conservation de
l'énergie totale nous permet d'obtenir l'expression de la mesure
algébrique de la vitesse : `v=sqrt(2g)sqrt(y_1-y)`.
• La
différentielle de l'abscisse curviligne est donnée par :
`ds=2Rcos(theta/2) d theta`
• Partant de :
`y=2Rsin^2(theta/2)`, on calcule :
`sin(theta/2)= -sqrt(y/(2R))`, le signe moins
tient au fait que `theta in [-pi,0]`.
- Calculons la
différentielle de y :
`dy=2Rsin(theta/2)cos(theta/2) d theta`.
- Il vient : `dy=sin(theta/2) ds rArr dy = -sqrt(y/(2R))ds`.
- Et : `ds= -(dy)/sqrt(y/(2R))`.
• Enfin, il vient :
`dt=-(dy)/(sqrt(2g)sqrt(y/(2R))sqrt(y_1-y))`.
• Soit : `color(navy)
(dt = -sqrt(R/g) (dy)/sqrt(y(y_1-y)))`.
• On écrit :
`tau=-sqrt(R/g) int_(y_1)^0 (dy)/sqrt(y(y_1-y))`.
- Or : `y(y_1-y)=(y_1/2)^2 (1-(2y/y_1-1)^2) rArr tau=-2/y_1 sqrt(R/g)
int_(y_1)^0 (dy)/sqrt(1-(2y/y_1-1)^2)`.
- Posons :
`v=2y/y_1-1`, alors `dy=y_1/2 dv`, et pour `y=y_1 rArr v=1`, et pour
`y=0 rArr v=-1`.
- Il vient :
`tau=-sqrt(R/g)
int_1^(-1) (dv)/sqrt(1-v^2)`, soit `tau=sqrt(R/g) int_(-1)^1
(dv)/sqrt(1-v^2)`.
Remarque : À
l'évidence ce calcul ne dépend pas des conditions
initiales en `M_1(x_1,y_1) ` ! La cycloïde
est bien une
courbe
tautochrone.
• Terminons le calcul :
`tau=sqrt(R/g) [arcsin(v)]_-1^1 rArr
tau=sqrt(R/g)[pi/2-(-pi/2)]`.
• D'où :
`color(navy)(tau=pi sqrt(R/g)`.

• L'image
ci-dessus, représente (ici) à la date t=0 s, trois masses
ponctuelles
initialement au repos, qui se déplacent sur une cycloïde
dont la représentation paramétrique est donnée par
:
`x=R(theta+sin(theta))`.
`y=R(1-cos(theta))`.
- Où : `theta
in [-pi,0]`.
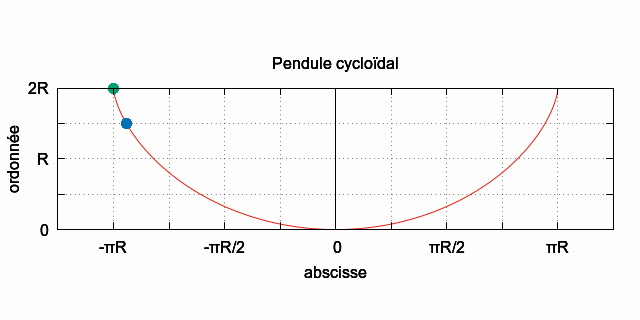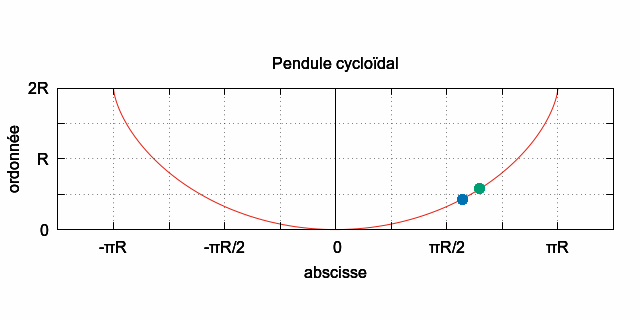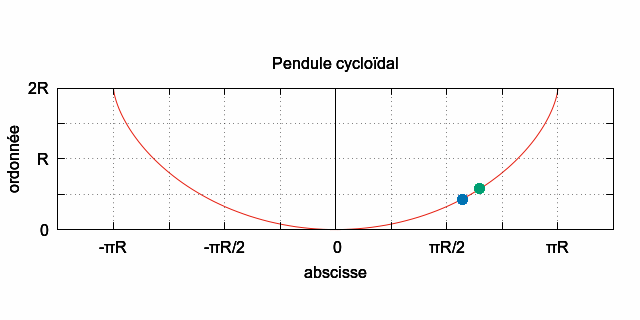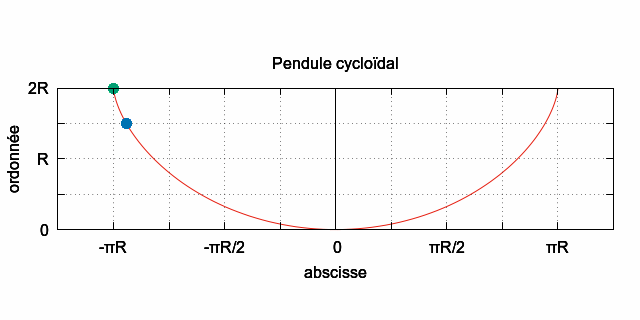
• La position à
la date t = 0 s de la masse ponctuelle :
- rouge, correspond
à : `color(red) (theta=-pi)`.
- verte, correspond
à : `color(green) (theta=-(2pi)/3)`.
- bleue, correspond
à : `color(blue) (theta=-pi/2)`.
• L'animation qui suit,
montre que la
cycloïde
est une courbe
tautochrone. Regarder l'animation...
• C'est un système physique que désormais, nous
connaissons bien...
• Une masse
ponctuelle m
glisse sans
frottement sur une cycloïde, sous l'influence de la gravité.
• La cycloïde a
comme représentation paramétrique :
`x=R(theta+sin(theta))`
`y=R(1-cos(theta)) hArr y=2Rsin^2(theta/2)`
- Où : `theta in [-pi,pi]`.
- On rappelle que l'abscisse curviligne du point M mesurée
à partir de l'origine O est donnée par :
`s_M=4Rsin(theta/2)`.
• On propose
d'étudier les
équations du mouvement de la masse ponctuelle en fonction de
l'abscisse curviligne.
• Dans ce
système physique, seul le poids `vec P` de la masse m travaille, en
effet la réaction `vec N`du support est perpendiculaire à
son dépacement, il y a donc conservation de l'énergie
totale du système physique.
`E=1/2 mv^2 +mgy` est constante.
• Exprimons
l'énergie totale du système physique, en fonction de
l'abscisse curviligne et de ses dérivées :
- On a : `v=(ds_M)/(dt) rArr v^2=((ds_M)/(dt))^2`.
- On a également : `y=R(1-cos(theta)) rArr y=2Rsin^2(theta/2)`,
et `y=(s_M ^2)/(8R)`.
• Alors
l'énergie totale a comme expression : `color(navy) (E=1/2
m((ds_M)/(dt))^2+"mg" (s_M ^2)/(8R))`.
• Calculons la
dérivée de l'énergie totale par rapport au temps.
- Comme l'énergie totale est constante, il vient : `(dE)/(dt)=0`.
- Et : `(dE)/(dt)=m (ds_M)/(dt) (d^2 s_M)/(dt^2)+(mg)/(4R) (ds_M)/(dt)
s_M rArr (dE)/(dt)=m (ds_M)/(dt)( (d^2 s_M)/(dt^2)+g/(4R) s_M)`.
- Comme : `(dE)/(dt)=0`, et dans la mesure où `(ds_M)/(dt) != 0`,
il vient :
`(d^2 s_M)/(dt^2)+g/(4R) s_M=0`.
• Posons :
`color(navy) (Omega^2=g/(4R))`, où `Omega` désigne une
pulsation, avec
`Omega= (2pi)/T`, où `T` est une période telle que
`color(navy) (T=4 pi sqrt(R/g))`.
• L'équation
différentielle ordinaire du second ordre s'ecrit alors :
`color(navy) ((d^2 s_M)/(dt^2)+Omega^2 s_M=0)`.
• Cette équation
admet une solution de la forme : `color(navy) (s_M=C_1 sin(Omega t)+C_2
cos(Omega t))`.
- Où `C_1` et `C_2` sont deux constantes d'intégration
à déterminer en fonction de conditions initiales prises
par le
système physique.
• L'abscisse curviligne
`s_M= bar "OM"` qui décrit le mouvement de la masse ponctuelle m est une
fonction sinusoïdale du temps, de période T.
• La masse ponctuelle m oscille de
manière sinusoïdale de
part et d'autre de l'origine O, en suivant la
cycloïde.
• Notons que la période
des oscillations est
indépendante des conditions initiales
imposées au système physique ; ce qui justifie une fois
encore que la
cycloïde soit une courbe tautochrone.
Remarque : Dans
l'étude menée au paragraphe 1.,
nous avons trouvé pour `tau` : `tau=pi sqrt(R/g)` ; on observe
que `tau=T/4`, où `T` est la période du pendule
étudié au paragraphe 2. ;
cela n'a rien d'étonnant car dans l'étude du paragraphe 1.,
on ne prend en compte que le quart de la période
d'oscillation !
Remarque : Animation réalisée à l'aide du logiciel gnuplot®.
• Cette page
n'aurait pas pu être composée sans les "outils" fournis
par AsciiMath, à l'URL
: <http://asciimath.org/>.
• Cette page a pu
être développée et affichée correctement
grâce à l'utilisation du réseau de distribution de
contenu MathJax (CDN). Toute
la documentation relative à MathJax
est accessible à l'URL :
<http://docs.mathjax.org/en/latest/index.html>.
• Les graphes et les
animations ont
été tracés à l'aide du logiciel
gnuplot®, dont la documentation est
accessible à l'URL :
<http://www.gnuplot.info/>.
Retour à la page précédente...