• En utilisant le calcul variationnel (c’est également le principe de FERMAT), on souhaite déterminer le chemin d’un rayon lumineux injecté dans le cœur, suivant l’axe de symétrie, et dans le plan méridien, d’une fibre optique à gradient d’indice linéaire.

• Le rayon lumineux
est "injecté" dans la fibre au point O
qui appartient à l'axe de symétrie de la fibre optique de
forme cylindrique, et dans le plan (xOz).
• Dans l'air, d'indice
optique n0, le rayon fait
l'angle θ0 avec l'axe de
symétrie de la fibre
optique.
• Dans le cœur
de la fibre
optique dont l'indice optique au voisinage de l'axe de symétrie
de cette même fibre est n1, le rayon
lumineux fait
l'angle θ1.
• Suivant l'axe des
abscisses Ox, l'indice optique du cœur de la fibre optique, est
une "fonction linéaire" d'équation :
`n(x)=n_1(1-(Delta|x|)/r_0)`.
- Où `Delta` est la variation relative
d'indice, avec : `Delta=(n_1-n_2)/(n_1)` , où `r_0` est le
rayon du cœur de la fibre optique.
• On donne les
caractéristiques optiques de la fibre : n1 = 1,50,
`Delta`= 1 %,
on en déduit n2 = 1,485.
• On donne les
caractéristiques géométriques de la fibre optique
:
- Diamètre du cœur : 50 µm (r0 =
25 µm), diamètre extérieur de la gaine (d'indice n2
constant) : 125 µm.

Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot®.
• On souhaite que la durée de parcours du rayon lumineux suivant son chemin soit extrémale (ici minimale) pour passer d'un point `M_1(x_1,z_1)` à un point `M_2(x_2,z_2)`.

• Pour parcourir
l'abscisse curviligne élémentaire `ds`, le rayon lumineux
met la durée `dt` telle que : `dt=(ds)/v_varphi`, où
`v_varphi` est la vitesse de phase de l'onde associée au rayon
lumineux.
- Or `v_varphi=c/n`, où `c` est la
célérité de la lumière dans le vide, et `n`
l'indice optique de la substance au point considéré.
• Il vient :
`dt=n/cds`, avec ici `ds=sqrt(dx^2+dz^2)`, soit `ds=sqrt(1+dotx^2)dz`,
où `dotx=(dx)/dz`, avec `n(x)=n_1(1-(Delta|x|)/r_0)`.
- Soit :
`dt=n_1/c (1-(Delta|x|)/r_0)sqrt(1+dotx^2)dz`.
• La durée du
parcours entre les points `M_1` et `M_2` est égale à :
`t_2-t_1=int_(z_1)^(z_2) n_1/c (1-(Delta|x|)/r_0)sqrt(1+dotx^2)dz`,
cette durée doit être extrémale (ici minimale) ;
c'est cette contrainte qui constitue le principe de FERMAT.
• La solution de ce
problème peut être obtenue à partir des
résultats du calcul des variations, car ici on doit trouver le
chemin (le parcours du rayon lumineux) qui rend cette intégrale
extrémale.
• Dans
l'intégrale précédente, la quantité :
`n_1/c (1-(Delta|x|)/r_0)sqrt(1+dotx^2)`, est la fonctionnelle de
cette intégrale.
• Cette fonctionnelle
s'écrit de manière générale `F(z,x,dotx)`,
où `z` est la variable d'intégration.
• On observe ici que
la fonctionnelle ne dépend pas explicitement de la variable
d'intégration `z`, ce qui aura une "heureuse
conséquence"…
• On écrit
alors : `color(navy)(F(x,dotx)=n_1/c (1-(Delta|x|)/r_0)sqrt(1+dotx^2))`.
• EULER a démontré que
pour rendre l'intégrale extrémale, sa fonctionnelle
devait vérifier :
`ul((delF(z,x,dotx))/(delx)-(d((delF(z,x,dotx))/(deldotx)))/dz=0)`.
• BELTRAMI a également
démontré que si la fonctionnelle ne dépendait pas
explicitement de la variable d'intégration, alors elle
vérifiait l'équation suivante :
`ul(F(x,dotx)-dotx
(delF(x,dotx))/(deldotx)=C_0)`, où `C_0` est une constante
d'intégration définie par une condition initiale.
• Ici :
`(delF(x,dotx))/(deldotx)=n_1/c (1-(Delta|x|)/r_0)
dotx/sqrt(1+dotx^2)`.
• L'équation de
BELTRAMI nous conduit à
écrire : `n_1/c (1-(Delta|x|)/r_0) (sqrt(1+dotx^2)-
dotx^2/sqrt(1+dotx^2))=C_0`, soit `n_1/c
((1-(Delta|x|)/r_0))/sqrt(1+dotx^2)=C_0`.
• Supposons que l'injection du rayon lumineux se fasse à l'origine O, sous un angle `theta_1` mesuré dans la fibre optique, par rapport à son axe de symétrie.

- Au point O de
coordonnées : `x=0`, `z=0`, dans le cœur de la fibre, on
peut écrire : `dx/dz=tan(theta_1)`, d'où
`dotx=tan(theta_1)`.
- Il vient :
`(n_1/c)/sqrt(1+tan^2(theta_1))=C_0
`, soit `ul(C_0=n_1/c cos(theta_1))`.
• Finalement nous
devons résoudre :
`((1-(Delta|x|)/r_0))/sqrt(1+dotx^2)=cos(theta_1)`.
• Soit encore :
`(1-(Delta|x|)/r_0)^2=cos^2(theta_1)(1+dotx^2)`, d'où
`dotx^2=((1- (Delta|x|)/r_0)/cos(theta_1))^2-1`.
• La condition
d'injection de la lumière à l'entrée O dans le
cœur de la fibre, impose : `0<=x` et `0<=dotx`.
- Aussi on cherche à résoudre :
`dotx=sqrt(((1- (Delta|x|)/r_0)/cos(theta_1))^2-1)`.
- Tout cela n'a de sens que si :
`color(red)(0<=((1- (Delta|x|)/r_0)/cos(theta_1))^2-1)`, soit
`color(red)(|x|/r_0<=(1-cos(theta_1))/Delta)`.
- On souhaite que le rayon soit guidé dans le
cœur de la fibre, ce qui impose de vérifier :
`|x/r_0|<=1`, soit encore, `1-Delta<=cos(theta_1)`.
• Alors
`color(navy)(theta_1in[0,theta_(1_lim)])`, avec
`color(navy) ul(theta_(1_lim)=arccos(1-Delta))`.
- Cette dernière relation définit la
condition de guidage
de la lumière dans le cœur de la fibre optique.
- Notons que l'on aura un extrémum
lorsque (`dotx=0`), et `x` sera alors égal à :
`|x_e|=r_0/Delta (1-cos(theta_1))`.
• Écrivons
maintenant : `u=(1- (Delta|x|)/r_0)/cos(theta_1)`, alors
`dotu=-Delta/(r_0cos(theta_1)) sgn(x)dotx`, avec
`dotu=(du)/(dz)`.
- Avec : `sign(x)=-1` si `x<0`, `sign(x)=0` si
`x=0`, `sign(x)=1` si `0<x`.
• Compte tenu ici de
la condition d'injection de la lumière `sign(x)=1`, et
`dotu=-Delta/(r_0cos(theta_1)) dotx`, d'où
`dotx=-(r_0cos(theta_1))/Delta dotu`.
- Il vient :
`-(r_0cos(theta_1))/Delta dotu=sqrt(u^2-1)`,
soit `dotu=-Delta/(r_0cos(theta_1))sqrt(u^2-1)`, et
`(du)/sqrt(u^2-1)=-Delta/(r_0cos(theta_1))dz`.
- L'intégration conduit à :
`argch(u)=-Delta/(r_0cos(theta_1))z+C_1`, où `C_1` est
une constante d'intégration.
- Alors :
`u=ch(C_1-Delta/(r_0cos(theta_1))z)`, et
`(1- (Delta|x|)/r_0)/cos(theta_1)=ch(C_1-Delta/(r_0cos(theta_1))z)`,
avec ici `|x|=x`.
- Il vient : `x=r_0/Delta
(1-cos(theta_1)ch(C_1-Delta/(r_0cos(theta_1))z))`.
- La condition initiale au point O, nous donne :
`x=0`, et `z=0` ; il vient `(1-cos(theta_1)ch(C_1))=0`, soit
`C_1=argch(1/cos(theta_1))`.
• On obtient
finalement l'expression de : `x=r_0/Delta
(1-cos(theta_1)ch(argch(1/cos(theta_1)) -Delta/(r_0cos(theta_1))z))`.
• Et l'expression de :
`dotx=sh(argch(1/cos(theta_1)) -Delta/(r_0cos(theta_1))z)`.
• Cherchons la
valeur
`z_e` pour laquelle `|x|=|x_e|` alors `x` passe par un extrémum,
et `dotx=0 rArr sh(argch(1/cos(theta_1))
-Delta/(r_0cos(theta_1))z_e)=0`.
- Alors : `ul(z_e=(r_0cos(theta_1))/Delta
argch(1/cos(theta_1)))`.
• Cherchons
l'expression de `dotx` en `z=0`, nous devrions trouver `tan(theta_1)` !
Rappel :
`argch(y)=ln(y+sqrt(y^2-1))` ; nous posons ici `y=1/cos(theta_1)`.
- On a : `dotx(0)=sh(argch(1/cos(theta_1)))`, soit
`dotx(0)= (e^(ln(y+sqrt(y^2-1))) -e^(-ln(y+sqrt(y^2-1))))/2`, puis
`dotx(0)= (y+sqrt(y^2-1) -1/(y+sqrt(y^2-1)))/2`, et
`dotx(0)=(y^2+ysqrt(y^2-1)-1)/(y+sqrt(y^2-1))`.
-
`dotx(0)=(1/cos^2(theta_1)+tan(theta_1)/cos(theta_1)-1)/(1/cos(theta_1)+tan(theta_1))`,
puis
`dotx(0)=(tan^2(theta_1)+tan(theta_1)/cos(theta_1))/(1/cos(theta_1)+tan(theta_1))`,
soit `dotx(0)=tan(theta_1)` !
Notons :
`color(navy) (tan(theta_1)=sh(argch(1/cos(theta_1))))`.
• Cherchons la
valeur
`z_(Lamda/2)` pour laquelle `dotx(z_(Lamda/2))=-tan(theta_1)` ; le
rayon lumineux fait l'angle `-theta_1` par rapport à la
direction de l'axe de symétrie de la fibre optique.
-
On a : `dotx(z_(Lamda/2))=sh(argch(1/cos(theta_1))
-Delta/(r_0cos(theta_1))z_(Lamda/2))`, on doit résoudre
`sh(argch(1/cos(theta_1))
-Delta/(r_0cos(theta_1))z_(Lamda/2))=-tan(theta_1)`.
-Soit : `sh(argch(1/cos(theta_1))
-Delta/(r_0cos(theta_1))z_(Lamda/2))=-sh(argch(1/cos(theta_1)))`, il
vient `z_(Lambda/2)=2(r_0cos(theta_1))/Delta argch(1/cos(theta_1))`,
soit encore `ul(z_(Lamda/2)=2z_e)`.
• Calculons
: `x(z_(Lambda/2))=r_0/Delta
(1-cos(theta_1)ch(argch(1/cos(theta_1))
-Delta/(r_0cos(theta_1))2(r_0cos(theta_1))/Delta
argch(1/cos(theta_1))))`.
- `x(z_(Lambda/2))=r_0/Delta
(1-cos(theta_1)ch(-argch(1/cos(theta_1)))`, `x(z_(Lambda/2))=r_0/Delta
(1-cos(theta_1)ch(argch(1/cos(theta_1)))`, et `x(z_(Lambda/2))=0` !
• Étude de
: `x(z)` pour `zin[0,z_(Lamda/2)]` :

Représentation graphique
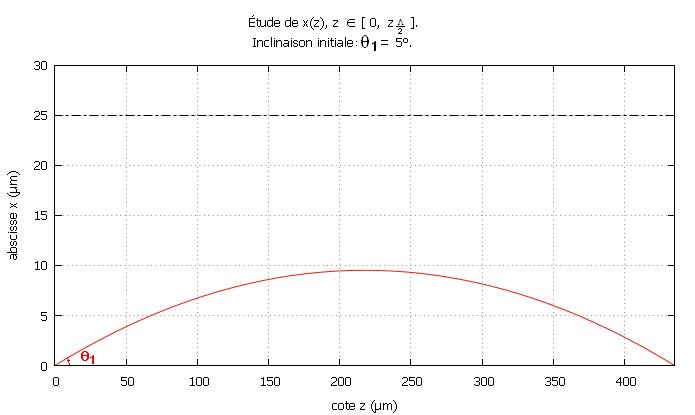
Remarque : Ce graphe a été tracé à l'aide du logiciel gnuplot® ; ici les échelles sur l'axe des abscisses et l'axe des cotes sont différentes ! C'est pourquoi, à l'origine O, l'angle entre l'axe des cotes (c'est aussi l'axe de symétrie de la fibre optique) et le rayon lumineux semble erroné...
• Le rayon lumineux
va
"osciller" autour de l'axe de symétrie de la fibre optique.
• Pour construire le
chemin suivi par le rayon il faut prolonger ce graphe.
Remarque : Posons
`z_Lamda=2z_(Lambda/2)`.
-
Pour `zin[0,z_(Lambda/2)]`, on tracera `x(z)=r_0/Delta
(1-cos(theta_1)ch(argch(1/cos(theta_1)) -Delta/(r_0cos(theta_1))z))`.
-
Pour `zin[z_(Lambda/2),z_Lambda]`, on tracera `-x(z-z_(Lambda/2))` ;
c'est la fonction `x(z)` "retardée" de `z_(Lambda/2)` et
changée de signe.
-
Pour `zin[z_Lambda,3z_(Lambda/2)]`, on tracera `x(z-z_Lambda))`.
-
Pour `zin[3z_(Lambda/2),2z_Lambda]`, on tracera `-x(z-3z_(Lambda/2))`
.etc.
• Le rayon lumineux
suit un chemin périodique, de période spatiale
`Lambda=z_Lambda`, avec `Lamda=4(r_0cos(theta_1))/Delta
argch(1/cos(theta_1))`.
• Pour
générer le graphe de `x(z)`, on programme en langage
C la
fonction `x(z)` pour `zin[0,z_(Lambda/2)]` et on prend en compte la
méthode à mettre en œuvre pour prolonger le graphe.
• Je
vous
propose de consulter un document html que j'ai rédigé
à votre intention et qui traite de la "Programmation de
l'équation du chemin suivi par la lumière pour la fibre
optique
à
gradient d'indice linéaire.", rendez-vous à la page
"GILBEL"...
• Le chemin suivi
par
le rayon lumineux est périodique, et pour `zin[0,z_(Lamda/2)]`
on a : `color(navy) ul(x(z)=r_0/Delta
(1-cos(theta_1)ch(argch(1/cos(theta_1)) -Delta/(r_0cos(theta_1))z)))`,
fonction que l'on prolonge comme nous l'avons montré.
- Nous obtenons bien ici l'expression analytique
du chemin suivi par le rayon lumineux.
- L'amplitude est égale à :
`color(navy) ul(r_0/Delta (1-cos(theta_1)))`, et la période
spatiale
à : `color(navy) ul(Lamda=4(r_0cos(theta_1))/Delta
argch(1/cos(theta_1)))`.
• Comme le montre les
figures des paragraphes
1. et 2.4.2., on
injecte le rayon lumineux sur la face d'entrée de la fibre
optique.
- Cette même face d'entrée est
"plongée"
dans l'air d'indice `n_0` ; et on y vérifie la loi de DESCARTES
: `n_0sin(theta_0)=n_1sin(theta_1)`.
- La condition de guidage
de la lumière dans le cœur de la fibre optique
impose `theta_1<=arccos(1-Delta)`.
- Aussi l'angle `theta_0` doit-il vérifier :
`sin(theta_0)<=n_1/n_0 sin(arccos(1-Delta))`, et `color(navy)
(theta_0in[0,theta_(0_lim)])` avec `color(navy)
ul(theta_(0_lim)=arcsin(n_1/n_0 sin(arccos(1-Delta))))`.
- Cette dernière relation définit la
condition
d'injection de la lumière sur la face d'entrée de la
fibre optique.
• Application
numérique : Avec `Delta= 1 %`, `n_1=1,5` et
`n_2=1,485`, il vient :
- `theta_(0_lim)=arcsin(n_1/n_0
sin(arccos(1-Delta)))` ; ici
`theta_(0_lim)=0.21321280348 rd`, soit
`theta_(0_lim)=12°12'58''`.
- `theta_(1_lim)=arccos(1-Delta)` ; ici
`theta_(1_lim)=0.14154 rd`, soit `theta_(1_lim)=8°06'34''`.
• La figure
suivante
représente le chemin suivi par la lumière dans le
cœur de la fibre optique pour :
- En rouge : `color(red)(theta_1=3°)`, en vert :
`color(green)(theta_1=5°)`, en bleu :
`color(blue)(theta_1=8°06'34'')`.

Remarque : Ces graphes ont été tracés à l'aide du logiciel gnuplot® ; ici les échelles sur l'axe des abscisses et l'axe des cotes sont différentes ! C'est pourquoi, à l'origine O, l'angle entre l'axe des cotes (c'est aussi l'axe de symétrie de la fibre optique) et le rayon lumineux semble erroné...
• Ici, nous ne
"profitons plus" de la relation de BELTRAMI,
mais nous allons
développer la relation de EULER
pour obtenir un système
d'équations différentielles ordinaires
(EDO) du premier ordre , que nous intégrerons
"numériquement" en mettant en œuvre la méthode de
RUNGE-KUTTA d'ordre quatre (RK4,4).
• La méthode de RUNGE-KUTTA RK4,4 est une
méthode numérique permettant de résoudre dans le
cas le plus général, un système d'équations
différentielles ordinaires (EDO) du premier ordre par
approximation. Cette méthode a été mise au point
par les mathématiciens Carl
RUNGE et Martin Wilhelm KUTTA.
- Rappelons qu'une équation
différentielle ordinaire (EDO) de degré n, est de la
forme :
`F(x,y(x),doty(x),ddoty(x),...,y^((n)) (x))=0`, où `y^((n)) (x)`
est
la derivée n-ième de `y(x)` par rapport à `x`.
- Pour une équation différentielle
ordinaire du premier ordre, on calcule la solution de l'équation
différentielle par itération, le raffinement de la
méthode conduit à une erreur d'ordre quatre.
- Lorsque l'on a affaire à une
équation différentelle ordinaire d'ordre n
supérieur ou égal à deux, on peut la
décomposer en un système
de n équations
différentielles ordinaires du premier ordre. On constitue alors
un espace vectoriel des solutions, de dimension fini ; on dit que
l'équation différentielle ordinaire de degré n est une
fonction à valeur vectorielle. Bien entendu, la méthode
de RUNGE-KUTTA RK4,4
s'applique à chaque composante vectorielle.
• La relation de EULER :
`(delF(x,dotx))/(delx)-(d((delF(x,dotx))/(deldotx)))/(dz)=0`.
• Expression analytique de la fonctionnelle :
`F(x,dotx)=n_1/c (1-(Delta|x|)/r_0)sqrt(1+dotx^2)`, qui ne
dépend pas ici explicitement de la variable `z`.
• Nous avons vu que si la
fonctionnelle ne dépendait pas explicitement de la variable (ici
`z`), alors la relation de EULER
s'exprimait sous la forme :
`color(navy) ((delF(x,dotx))/(delx)-dotx
(del^2 F(x,dotx))/(delx
deldotx)-ddotx
(del^2F(x,dotx))/(del dotx^2)=0)`.
- Avec : `(delF(x,dotx))/(delx)=-n_1/c Delta/r_0
sqrt(1+dotx^2)sgn(x)` ;
`(delF(x,dotx))/(deldotx)=n_1/c (dotx(1-(Delta|x|)/r_0))/sqrt(1+dotx^2`
; `(del^2F(x,dotx))/(delxdeldotx)=-n_1/c Delta/r_0
(dotxsgn(x))/sqrt(1+dotx^2)` ;
`(del^2F(x,dotx))/(deldotx^2)=n_1/c
((1-(Delta|x|)/r_0))/((1+dotx^2)sqrt(1+dotx^2))`.
• On doit donc résoudre : `-n_1/c
Delta/r_0 (dotxsgn(x))/sqrt(1+dotx^2)+n_1/c Delta/r_0 (dotx^2
sgn(x))/sqrt(1+dotx^2)-n_1/c
(ddotx(1-(Delta|x|)/r_0))/((1+dotx^2)sqrt(1+dotx^2))=0`.
• Après simplification, il vient :
`color(navy) ul(ddotx=-Delta/r_0
((1+dotx^2)sgn(x))/(1-(Delta|x|)/r_0))`.
- Nous avons affaire à une équation
différentielle ordinaire du second ordre.
• Nous ramenons cette équation
différentielle du second ordre, à un système de
deux équations différentielles du premier ordre
• Posons : `ul(x=u_0)`, et
`(du_0)/(dz)=u_1` ; on en déduit `u_1=(dx)/(dz)`, soit
`ul(dotx=u_1)` et `(du_1)/(dz)=(d dotx)/(dz)`, soit
`ul(ddotx=(du_1)/(dz))`.
• L'équation différentielle
du second ordre s'écrit alors : `(du_1)/(dz)=-Delta/r_0
((1+u_1^2)sgn(u_0))/(1-(Delta|u_0|)/r_0)`.
• Nous devons donc résoudre le
systèmes de deux équations différentielles
ordinaires du premier ordre suivant :
`color(navy)((du_0)/(dz)=u_1)`
`color(navy)((du_1)/(dz)=-Delta/r_0
((1+u_1^2)sgn(u_0))/(1-(Delta|u_0|)/r_0))`
- Où : `u_0=u_0(z)` et `u_1=u_1(z)` sont des
fonctions de la
variable `z`.
Remarque : On a
affaire à un système d'équations couplées.
• Dans la méthode de RUNGE-KUTTA RK4,4, on
programme le système des deux équations
différentielles ordinaires du premier ordre, et l'on
précise les conditions initiales (ici au nombre de deux).
• À l'entrée de la fibre
optique, au point O,
`z=0`, et `x=0 rArr u_0(0)=0`, et
`(dx)/(dz)=tan(theta_1) rArr u_1(0)=tan(theta_1)`.
• On choisit
`theta_1<=theta_(1_lim)` ; cette "heureuse" hypothèse
résulte du calcul mené avec la méthode de BELTRAMI...
• `z` prend ses valeurs dans l'intervalle
`[0, z_(Max)]`, et varie au pas `Deltaz`.
• L'algorithme de la méthode de RUNGE-KUTTA RK4,4
élabore une "table de données" constituée de n lignes
contenant chacune le triplet : {`z, u_0(z), u_1(z)`}.
- On résoud
bien notre problème sous forme numérique, et
l'exploitation de la "table de données" permet ici de tracer
les chemins suivis par la lumière dans le cœur de la fibre
optique.
• On choisit `theta_1<=theta_(1_lim)`,
on impose `u_0(0)=0` et `u_1(0)=tan(theta_1)`.
• Ici `z_(Max)=1700` µm, le
pas est égal à `Deltaz=0,17` µm, la variation
relative d'indice est égale à `Delta=1 %`, le rayon du
cœur de la fibre
optique est égal à `r_0= 25` µm.
- On obtient alors une "table de données"
formée de dix mille lignes, constituées chacune du
triplet : {`z,u_0(z),u_1(z)`}.
- On donne à `theta_1` différentes
valeurs :
- En rouge : `color(red)(theta_1=3°)`, en vert :
`color(green)(theta_1=5°)`, en bleu :
`color(blue)(theta_1=8°06'34'')`.

Remarque
: Ces
graphes ont été tracés à l'aide du logiciel
gnuplot®
; ici les échelles sur l'axe des abscisses et l'axe
des cotes sont différentes ! C'est pourquoi, à l'origine O, l'angle entre
l'axe des cotes (c'est aussi l'axe de symétrie de la fibre
optique) et le rayon lumineux semble erroné…
• Les graphes obtenus par
intégration numérique de l'équation
différentielle ordinaire du second ordre par la méthode
de RUNGE-KUTTA RK4,4,
sont identiques à ceux obtenus de manière analytique par
intégration de l'équation de BELTRAMI !
• Il s'agit du tracé de
`dotx(z)` en fonction de
`x(z)`, en effet dans le triplet : {`z, u_0(z), u_1(z)`} ; on a :
`u_0(z)= x(z)` et `u_1(z)=dotx(z)`.
- On donne à `theta_1` différentes
valeurs :
- En rouge : `color(red)(theta_1=3°)`, en vert :
`color(green)(theta_1=5°)`, en bleu :
`color(blue)(theta_1=8°06'34'')`.

• Il est évident ici que les chemins suivis par la lumière sont bien périodiques dans l'espace, mais ils ne sont certainement pas sinusoïdaux !
• Dans la mesure où l'on cherche
à connaître le chemin suivi par la lumière dans le
cœur de la fibre
optique, l'utilisation de la méthode
de RUNGE-KUTTA RK4,4
nous facilite les calculs, en effet, on ne procède qu'à
des dérivations qui conduisent à établir un système des deux équations
différentielles ordinaires du premier ordre, et
l'on procède alors à l'intégration
numérique.
• Cependant, il faut formuler
correctement
le problème. Formulation qui nous impose ici d'utiliser le
calcul variationnel, qui se révèle être un outil
d'investigation "puissant"...
• J'adresse mes plus vifs
remerciements à Monsieur John
BURKARDT, Chercheur
invité du Département Informatique Scientifique, Florida State University (FSU) : John BURKARDT.
• Monsieur John
BURKARDT met à notre disposition, le code source
écrit en C, de la méthode
de RUNGE-KUTTA RK4,4,
sous le vocable rk4.c,
et un fichier d'en-tête rk4.h.
- Deux algorithmes sont
développés :
• "RK4 takes one Runge-Kutta step for a scalar ODE", qui permet de
résoudre une
équation différentielle ordinaire du premier ordre.
• "RK4VEC takes one Runge-Kutta step for a vector ODE", qui permet
de résoudre un système de n
équations différentielles ordinaires du premier ordre,
l'équation différentielle ordinaire d'ordre n à
l'origine de ce système de n
équations différentielles ordinaires du premier ordre,
est
"bien" une fonction à valeur vectorielle.
• Monsieur John
BURKARDT met également à notre disposition, le
code
source écrit en C, de deux exemples permettant de tester les
deux algorithmes proposés, sous le vocable rk4_prb.c.
- Les trois fichiers peuvent être
téléchargés à l'URL : <https://people.sc.fsu.edu/~jburkardt/c_src/rk4/rk4.html>.
• Pour ma
part, je vous
propose de consulter un document html que j'ai rédigé
à votre intention et qui traite de la "Mise en œuvre
pratique de la méthode RK4,4 pour la fibre optique
à
gradient d'indice linéaire.", rendez-vous à la page
"GILRK4"...
• Cette page n'aurait pas pu
être
composée sans les "outils" fournis par AsciiMath, à l'URL : <http://asciimath.org/>.
• Cette page a pu être
développée et affichée correctement grâce
à l'utilisation
du réseau de distribution de contenu MathJax (CDN). Toute la
documentation relative à MathJax
est accessible à l'URL : <http://docs.mathjax.org/en/latest/index.html>.
• Les graphes ont
été tracés à l'aide du logiciel
gnuplot®, dont
la documentation est accessible à
l'URL : <http://www.gnuplot.info/>.
Retour à la page principale...