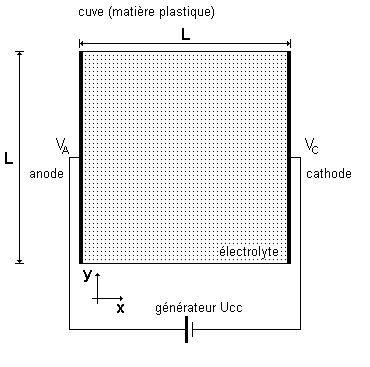
• Une cuve carrée dont le coté
est de longueur L, en
matière plastique, contient un électrolyte de
conductivité `sigma`.
• Une électrode (anode) rectiligne
portée au potentiel VA , plonge dans
l'électrolyte
à l'abscisse x = 0.
• Une électrode (cathode) rectiligne
portée au potentiel VC , plonge dans
l'électrolyte
à l'abscisse x = L.
• La différence de potentiel VA
- VC =
UCC est maintenue constante par un générateur
de tension
continue.
• On souhaite obtenir la cartographie du
potentiel électrique, au sein de l'électrolyte.
• On fait l'hypothèse que la hauteur de
l'électrolyte est "faible" de manière à ramener le
problème à deux dimensions, suivant l'abscisse x et
l'ordonnée y.
• Le courant par unité de surface `vec
j` au
sein de l'électrolyte est lié au champ électrique
`vec E` qui y règne par la relation : `vec j = sigma vec E`
où `sigma` désigne
la conductivité de l'électrolyte.
• Le courant I qui circule
dans l'électrolyte est continu, aussi vérifie-t-il la
relation : `"div"(vec j) = 0`.
• Or : `vec j = sigma vec E`, d'où
`"div"(sigma vec E) = 0` ; on fait l'hypothèse que `sigma` ne
dépend pas des coordonnées de position, il vient alors :
`"div"(vec E)= 0`.
• Le champ électrique `vec E`
dérive du potentiel scalaire `V` qui règne au sein de
l'électrolyte, et on écrit : `vec E = - vec "grad" (V)`.
• Or : `"div"(vec E)=0`, il vient `"div"(-vec
"grad" (V))=0`, soit ` -DeltaV=0`, où `Delta` désigne le
LAPLACIEN ; on obtient l'équation de POISSON
: `color(navy) (DeltaV=0)`.
• Nous avons fait l'hypothèse que le
problème est à deux dimensions, nous devons donc
résoudre : `color(navy) ((del^2V)/(delx^2)+(del^2V)/(dely^2)=0)`.
• Pour `x=0` on peut écrire
: `V(0,y) = V_A , AA y in [0,L]`.
• Pour `x=L` on peut écrire
: `V(L,y) = V_C , AA y in [0,L]`.
• La cuve contenant l'électrolyte
constitue un tube de courant limité par les bords libres de
cette même cuve.
• Aussi pour `y=0, AA x in[0,L]` , on
peut
écrire : `j_y=0 rArr E_y=0`, avec `vec E = -vec "grad" (V)` , il
vient : `((delV)/(dely))_(x,0)=0`.
• De même, pour `y=L, AA x in[0,L]` , on peut
écrire : `j_y=0 rArr E_y=0`,
avec `vec E = -vec "grad" (V)` , il vient : `((delV)/(dely))_(x,L)=0`.
Remarque : La
cuve électrolytique est un carré dont le coté est
de longueur L.
• Suivant l'abscisse x, on divise le coté de longueur L en
NMax intervalles.
- L'extension d'un intervalle
suivant les abscisses est donc : `Deltax = L/(N_(Max))`.
- Un point d'abscisse `x` est
repéré par l'index `i` tel que : `x=x_i` avec `x_i=i Delta
x` où `i in [0,N_(Max)]`.
• Suivant l'ordonnée y, on divise le coté de
longueur L en
NMax intervalles.
- L'extension d'un intervalle
suivant les ordonnées est donc : `Deltay = L/(N_(Max))`.
- Un point d'ordonnée `y`
est repéré par l'index `j`
tel que : `y=y_j` avec `y_j=j Delta y` où `j in [0,N_(Max)]`.
• On observe ici que `Deltax=Deltay` , on note `Deltah` la valeur
commune de l'extension d'un intervalle.
• Pour `i=0` on peut écrire : `V(x_0,y_j)=V_A ,
AA j in[0,N_(Max)]` ; soit encore : `color(navy)
(V_(0,j)=V_A , AA j in[0,N_(Max)])`, où on a remplacé x0 par son index i=0, et
où
on a remplacé yj par son index j.
• Pour `i=N_(Max)` on peut écrire
: `V(x_(N_(Max)),y_j)=V_C , AA j in[0,N_(Max)]` ;
soit encore : `color(navy) (V_(N_(Max),j)=V_C , AA j
in[0,N_(Max)])`, où
on a
remplacé xNMax par son index i=NMax, et où on a
remplacé yj par son index j.
• Pour `j=0, AA i in[1,N_(Max)-1]` , on peut
écrire : `((delV)/(dely))_(x_i,y_0)=0` .
- Pour évaluer : `((delV)/(dely))_(x_i,y_0)=0`, on
calcule la dérivée "vers le haut"...
- Il vient : `((delV)/(dely))_(x_i,y_0)=(V(x_i,
y_0+Deltay)-V(x_i, y_0))/(Deltay)` ; ou
`((delV)/(dely))_(x_i,y_0)=(V(x_i, y_(0+1))-V(x_i, y_0))/(Deltay)` .
- Soit encore :
`((delV)/(dely))_(x_i,y_0)=(V_(i,1)-V_(i,0))/(Deltay)` , avec `((delV)/(dely))_(x_i,y_0)=0`.
- Il vient enfin : `color(navy) (V_(i,0)=V_(i,1), AA i in
[1,N_(Max)-1])`.
NB : On fait l'hypothèse que l'on connaît `color(red)
(V_(i,1))`.
• Pour `j=N_(Max), AA i in[1,N_(Max)-1]` , on peut
écrire `((delV)/(dely))_(x_i,y_(N_(Max)))=0` .
- Pour évaluer
`((delV)/(dely))_(x_i,y_(N_(Max)))=0`, on calcule la
dérivée "vers le bas"...
- Il vient :
`((delV)/(dely))_(x_i,y_(N_(Max)))=(V(x_i,y_(N_(Max))) -
V(x_i,y_(N_(Max))-Deltay))/(Deltay)` ; ou
`((delV)/(dely))_(x_i,y_(N_(Max)))=(V(x_i,y_(N_(Max)))-V(x_i,y_(N_(Max)-1)))/(Deltay)`
.
- Soit encore :
`((delV)/(dely))_(x_i,y_(N_(Max)))=(V_(i,N_(Max))-V_(i,N_(Max)-1))/(Deltay)`
, avec `((delV)/(dely))_(x_i,y_(N_(Max)))=0`.
- Il vient enfin : `color(navy) (V_(i,N_(Max))=V_(i,N_(Max)-1),
AA i in [1,N_(Max)-1])`.
NB : On
fait l'hypothèse que l'on connaît
`color(red) (V_(i,N_(Max)-1))`.
Remarque : Nous
avons remplacé les dérivées partielles par des
différences finies...
• On calcule tout d'abord : `((del^2V)/(delx^2))_(x_i,y_j)` ; soit
`((del((delV)/(delx)))/(delx))_(x_i,y_j)`.
- On calcule la dérivée première, partielle,
centrée : `((delV)/(delx))_(x_i,y_j)` ; il vient :
`((delV)/(delx))_(x_i,y_j)=(V(x_i+(Deltax)/2,y_j)-V(x_i-(Deltax)/2,y_j))/(Deltax)`.
- On calcule la dérivée seconde, partielle,
centrée : `((del((delV)/(delx)))/(delx))_(x_i,y_j)` ; il
vient :
`((del((delV)/(delx)))/(delx))_(x_i,y_j)=((V(x_i+Deltax,y_j)-V(x_i,y_j)-V(x_i,y_j)+V(x_i-Deltax,y_j))/(Deltax))/(Deltax)`
- Soit encore :
`((del^2V)/(delx^2))_(x_i,y_j)=(V(x_i+Deltax,y_j)-V(x_i,y_j)-V(x_i,y_j)+V(x_i-Deltax,y_j))/(Deltax^2)`.
• On peut alors écrire : `color(navy)
(((del^2V)/(delx^2))_(x_i,y_j)=(V_(i+1,j)-2V_(i,j)+V_(i-1,j))/(Deltax^2))`.
• On écrirait de même : `color(navy)
(((del^2V)/(dely^2))_(x_i,y_j)=(V_(i,j+1)-2V_(i,j)+V_(i,j-1))/(Deltay^2))`.
• On écrit l'équation de POISSON:
`((del^2V)/(delx^2))_(x_i,y_j)+((del^2V)/(dely^2))_(x_i,y_j)=(V_(i+1,j)-2V_(i,j)+V_(i-1,j))/(Deltax^2)+(V_(i,j+1)-2V_(i,j)+V_(i,j-1))/(Deltay^2)`.
• Ici : `Deltax =Deltay=Deltah`, et
`((del^2V)/(delx^2))_(x_i,y_j)+((del^2V)/(dely^2))_(x_i,y_j)=0`.
• Alors :
`(V_(i+1,j)-2V_(i,j)+V_(i-1,j)+V_(i,j+1)-2V_(i,j)+V_(i,j-1))/(Deltah^2)=0`.
• D'où : `color(navy)
(V_(i,j)=(V_(i+1,j)+V_(i-1,j)+V_(i,j+1)+V_(i,j-1))/4)`, avec
`color(navy) (i in[1,N_(Max)-1])` et `color(navy) (j in[1,N_(Max)-1])`.
• Les conditions initiales sont données par : `V_(0,j)=V_A
, AA j in[0,N_(Max)]`, et `V_(N_(Max),j)=V_C , AA j
in[0,N_(Max)]`.
• Pour `i in[1,N_(Max)-1]` et `j in[0,N_(Max)]`, on
initialise `V_(i,j)` à `V_(i,j)=(V_A + V_C)/2`.
• Dans une boucle que l'on répétera un "certain
nombre de fois"... on calcule :
`V_(i,0)=V_(i,1), AA i in
[1,N_(Max)-1]`.
`V_(i,N_(Max))=V_(i,N_(Max)-1),
AA i in [1,N_(Max)-1]`.
`V_(i,j)=(V_(i+1,j)+V_(i-1,j)+V_(i,j+1)+V_(i,j-1))/4` pour `i
in[1,N_(Max)-1]` et `j in[1,N_(Max)-1]`.
Remarque : Dans le
cas de l'équation de POISSON,
le procédé de calcul converge toujours...
• Nous représentons le potentiel `V=V(x,y)`, ce qui revient
à représenter une surface dans un espace à trois
dimensions, `V(x,y)` s'identifie alors avec la cote `z`, soit `V(x,y)
hArr
z`.
• Le domaine dans lequel les variables `x` et `y` prennent leurs
valeurs est constitué par le carré qui délimite la
cuve électrolytique ;
cependant ce sont les
équations de la physique qui
contraignent la "forme" que
prendra de la surface représentative
de `V(x,y)`.
Remarque : On donne
`V_A-V_C= 10` V, le coté du carré délimitant la
cuve électrolytique est
découpé en
`N_(Max)=50` parties égales.
- Ici on substitue
à
l'abscisse x=xi son
index i, et on substitue à
l'ordonnée y=yj son index j...

Remarque : Figure
tracée à l'aide du logiciel gnuplot®.
• Le potentiel `V(x,y)` décroît linéairement
suivant l'abscisse `x`, mais il ne varie pas avec l'ordonnée
`y`. Le résultat n'est pas surprenant dans la mesure où
nous avons affaire à un électrolyte homogène,
confiné dans une cuve électrolytique de
géométrie simple.
• Il est intéressant d'observer le fonctionnement de
l'algorithme mettant en œuvre la méthode des
différences
finies, aussi je vous renvoie vers l'animation...
• On cherche à déterminer le lieu des points de la
cuve électrolytique dont le potentiel a une valeur
donnée constante ; c'est ce que l'on fait de
manière expérimentale. On néglige la hauteur de
l'électrolyte, c'est pourquoi nous ne décrivons
le potentiel que suivant l'abscisse `x` et l'ordonnée `y`.
• Ici on substitue
à l'abscisse x=xi son
index i, et on substitue à
l'ordonnée y=yj son index j...

Remarque : Figure
tracée à l'aide du logiciel gnuplot®.
• Le résultat n'est pas surprenant ici, les lignes
équipotentielles sont parallèles aux deux
électrodes, une fois encore, nous avons affaire à un
électrolyte homogène,
confiné dans une cuve électrolytique de
géométrie simple.
• On peut décrire ces lignes équipotentielles par
l'équation : `V(x_i,y_j)=V_(i,j)` avec,
`V_(i,j)=((V_A - V_C))/50 (50-i)`, `i in [0,50]` `AA j in
[0,50]`.
• Nous devons développer un programme qui met en
œuvre
l'algorithme décrit au paragraphe 2.3. .
• L'idée est de créer un tableau à deux
"dimensions" contenant `(N_(Max) +1)^2` cellules que l'on adresse
grâce aux deux index i
et j ; chaque cellule contient
la valeur correspondante de `V_(i,j)`.
• Je vous propose de consulter un
document html que j'ai
rédigé à votre intention et qui traite de la "Mise
en œuvre pratique de la méthode des différences
finies pour la cuve électrolytique homogène", rendez-vous à
la page "MDFPOT"...

• Une cuve carrée dont le coté
est de longueur L, en
matière plastique, contient un électrolyte de
conductivité `sigma`.
• Une électrode
(anode) rectiligne
portée au potentiel VA , plonge dans
l'électrolyte
à l'abscisse x = 0.
• Une électrode
(cathode) rectiligne
portée au potentiel VC , plonge dans
l'électrolyte
à l'abscisse x = L
• La différence
de potentiel VA
- VC =
UCC est maintenue constante par un générateur
de tension
continue.
• On introduit au centre de la cuve, une plaque métallique
de "faible" épaisseur, de forme carrée, dont le
coté est de longueur l,
le métal a une conductivité `sigma_m`.
• On souhaite obtenir la cartographie du
potentiel électrique, au sein de l'électrolyte
désormais "perturbé"...
• On fait l'hypothèse que la hauteur de
l'électrolyte est "faible", que l'épaisseur de la plaque
métallique est également "faible", de manière
à ramener le
problème à deux dimensions, suivant l'abscisse x et
l'ordonnée y.
• Les équations établies pour la cuve
électrolytique homogène restent bien entendu valables.
• En particulier :
- Les électrodes constituent des lignes équipotentielles :
• Pour
`x=0`, on peut écrire :
`V(0,y) = V_A , AA y in [0,L]`.
• Pour `x=L`, on peut écrire :
`V(L,y) = V_C , AA y in [0,L]`.
- Les lignes de courant sont tangentes aux bords libres de la cuve :
• Pour `y=0, AA x in[0,L]`, on
peut
écrire : `((delV)/(dely))_(x,0)=0`.
• Pour `y=L, AA x in[0,L]`, on peut
écrire : `((delV)/(dely))_(x,L)=0`.
- L'équation de POISSON
est toujours vérifiée dans l'électrolyte : `DeltaV
=0`.
• En ce qui concerne
l'équation de POISSON
dans le métal, on pourrait démontrer que l'on
vérifie
encore : `DeltaV =0`.
- Soit : `(del^2V)/(delx^2)+(del^2V)/(dely^2)=0`.
• L'intensité du courant électrique qui circule dans
la plaque métallique est une fraction de l'intensité qui
circule dans tous le dispositif, aussi le courant par unité de
surface `color(navy) (vec j_m)` qui circule dans le métal a-t-il une valeur
finie.
• Le vecteur champ électrique dans le métal est
donné par la relation `vec E_m= (vec j_m)/sigma_m`.
• Hypothèse
: Nous
supposons que la conductivité `sigma_m` du métal est
"très grande", soit : `sigma_m -> oo`.
- Comme `vec E_m= (vec j_m)/sigma_m rArr vec E_m ->vec 0`, et nous
écrivons `vec E_m = vec 0`.
- Le champ électrique `vec E_m` dérive du potentiel
scalaire `V_m`.
- Il vient alors : `-vec "grad" (V_m) = vec 0` ; d'où `V_m =
V_0`,
où `V_0` est une constante.
- Le
potentiel
`color(navy) (V_m)` de la plaque métallique est constant.
• Le maillage de la cuve électrolytique :
- Suivant l'abscisse x, on divise le coté de longueur L en
NMax intervalles.
• L'extension d'un intervalle
suivant les abscisses est donc : `Deltax = L/(N_(Max))`.
• Un point d'abscisse `x` est
repéré par l'index `i` tel que : `x=x_i` avec `x_i=i Delta
x` où `i in [0,N_(Max)]`.
- Suivant l'ordonnée y, on divise le coté de longueur L en
NMax intervalles.
• L'extension d'un intervalle
suivant les ordonnées est donc : `Deltay = L/(N_(Max))`.
• Un point d'ordonnée `y` est
repéré par l'index `j` tel que : `y=y_j` avec `y_j=j Delta
y` où `j in [0,N_(Max)]`.
• Ici : `Deltax=Deltay` , on note `Deltah` la valeur
commune de l'extension d'un intervalle.
• Le maillage de la plaque métallique :
- On choisit de diviser l'axe des abscisses et l'axe des
ordonnées au pas `Deltah`.
• Aussi le nombre d'intervalles sur chacun des cotés de la
plaque métallique qui est un carré, sera-t-il égal
à : `N_(m_(Max))=l/(Deltah)`.
• Un point de la plaque métallique d'abscisse `x` est
repéré par l'index `i_m` tel que : `x=x_(i_m)` avec
`x_(i_m)=i_m Delta
h` où `i_m in [0,N_(m_(Max))]`.
•Un point de la plaque métallique d'ordonnée `y` est
repéré par l'index `j_m` tel que : `y=y_(j_m)` avec
`y_(j_m)=j_m Delta
h` où `j_m in [0,N_(m_(Max))]`.
• Équation de la physique concernant la cuve
électrolytique :
- Potentiel des électrodes :
• On écrit : `color(navy)
(V_(0,j)=V_A , AA j in[0,N_(Max)])`, où on a remplacé x0 par son index i=0, et
où
on a remplacé yj par son index j.
• On écrit : `color(navy) (V_(N_(Max),j)=V_C ,
AA j
in[0,N_(Max)])`, où
on a
remplacé xNMax par son index i=NMax, et où on a
remplacé yj par son index j.
- Les lignes de courant sont tangentes aux bords libres de la cuve
électrolytique :
• On écrit : `color(navy) (V_(i,0)=V_(i,1), AA i in
[1,N_(Max)-1])`.
• On écrit : `color(navy) (V_(i,N_(Max))=V_(i,N_(Max)-1),
AA i in [1,N_(Max)-1])`.
- Contrainte liée à l'équation de POISSON
:
• On écrit : `color(navy)
(V_(i,j)=(V_(i+1,j)+V_(i-1,j)+V_(i,j+1)+V_(i,j-1))/4)`, avec
`color(navy) (i in[1,N_(Max)-1])` et `color(navy) (j in[1,N_(Max)-1])`.
• Équation de la physique concernant la plaque
métallique :
- On place la plaque métallique au centre de la cuve
électrolytique :
• L'origine Om de la plaque métallique, par
rapport
à l'origine O de la cuve
électrolytique a comme coordonnées, comptées en
pas d'extension `Deltah` :
- Suivant les abscisses :
`(N_(Max)-N_(m_(Max)))/2`.
- Suivant les
ordonnées : `(N_(Max)-N_(m_(Max)))/2`.
• Aussi, pour la plaque métallique, les index prendront-ils
comme valeurs en pas d'extension `Deltah` :
- Pour `i_m` : `i_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2]`.
- Pour `j_m` : `j_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2]`.
• Comme le potentiel de la plaque métallique est constant :
- On écrit :
`color(navy)
(V_(i_m,j_m)=V_((N_(Max)-N_(m_(Max)))/2,(N_(Max)-N_(m_(Max)))/2))`,
avec `color(navy) (i_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2])`, et
`color(navy) (j_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2])`.
Remarque : Implicitement,
nous venons de donner l'algorithme de résolution du
problème !
• Les conditions initiales sont données par : `V_(0,j)=V_A
, AA j in[0,N_(Max)]`, et `V_(N_(Max),j)=V_C , AA j
in[0,N_(Max)]`.
• Pour `i in[1,N_(Max)-1]` et `j in[0,N_(Max)]`, on
initialise `V_(i,j)` à `V_(i,j)=(V_A + V_C)/2`.
• Dans une boucle que l'on répétera un "certain
nombre de fois"... on calcule :
`V_(i,0)=V_(i,1), AA i in
[1,N_(Max)-1]`.
`V_(i,N_(Max))=V_(i,N_(Max)-1),
AA i in [1,N_(Max)-1]`.
`V_(i_m,j_m)=V_((N_(Max)-N_(m_(Max)))/2,(N_(Max)-N_(m_(Max)))/2)`,
avec `i_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2]`, et
`j_m
in[(N_(Max)-N_(m_(Max)))/2,(N_(Max)+N_(m_(Max)))/2]`.
`V_(i,j)=(V_(i+1,j)+V_(i-1,j)+V_(i,j+1)+V_(i,j-1))/4` pour `i
in[1,N_(Max)-1]` et `j in[1,N_(Max)-1]`.
• Nous représentons le potentiel `V=V(x,y)`, ce qui revient
à représenter une surface dans un espace à trois
dimensions, `V(x,y)` s'identifie alors avec la cote `z`, soit `V(x,y)
hArr
z`.
• Le domaine dans lequel les variables `x` et `y` prennent leurs
valeurs est constitué par le carré qui délimite la
cuve électrolytique ;
cependant ce sont les
équations de la physique qui
contraignent la "forme" que
prendra de la surface représentative
de `V(x,y)`.
Remarque : On donne
`V_A-V_C= 10` V ; le coté du carré délimitant la
cuve électrolytique est
découpé en
`N_(Max)=50` parties égales.
- Le coté du carré délimitant la plaque
métallique est
découpé en
`N_(m_(Max))=10` parties égales.
- Ici on substitue
à
l'abscisse x=xi son
index i, et on substitue à
l'ordonnée y=yj son index j...
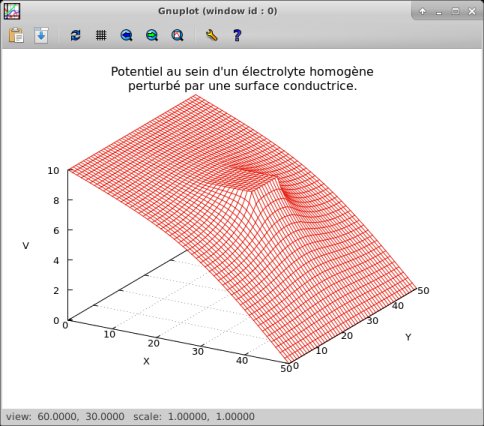
Remarque : Figure
tracée à l'aide du logiciel gnuplot®.
• Le potentiel `V(x,y)` est fortement modifié par la
présence de la plaque métallique qui apparaît ici
sous la forme d'un carré dont le potentiel est constant (voisin
ici de 8 volts) ; le potentiel `V(x,y)` varie maintenant en fonction de
l'abscisse x et de l'ordonnée y.
• Il est intéressant d'observer le fonctionnement de
l'algorithme mettant en œuvre la méthode des
différences
finies, aussi je vous renvoie vers l'animation...
• On cherche à déterminer le lieu des points de la
cuve électrolytique dont le potentiel a une valeur
donnée constante ; c'est ce que l'on fait de
manière expérimentale. On néglige la hauteur de
l'électrolyte, comme on néglige l'épaisseur de la
plaque métallique, c'est pourquoi nous ne décrivons
le potentiel que suivant l'abscisse `x` et l'ordonnée `y`.
• Ici on substitue
à l'abscisse x=xi son
index i, et on substitue à
l'ordonnée y=yj son index j...
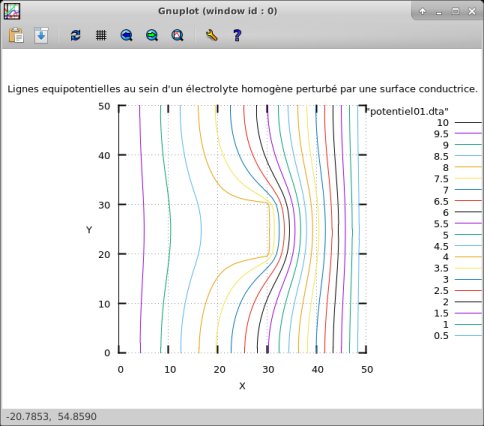
Remarque : Figure
tracée à l'aide du logiciel gnuplot®.
• Les lignes
équipotentielles ne sont pratiquement plus parallèles aux
deux
électrodes, elles sont fortement déformées par la
présence de la plaque métallique.
• L'équipotentielle "8 volts" épouse le contour de
la plaque métallique.
• Nous devons développer un programme qui met en
œuvre
l'algorithme décrit au paragraphe 3.5. .
• L'idée est de créer un tableau à deux
"dimensions" contenant `(N_(Max) +1)^2` cellules que l'on adresse
grâce aux deux index i
et j ; chaque cellule contient
la valeur correspondante de `V_(i,j)`.
• Je vous propose de consulter un
document html que j'ai
rédigé à votre intention et qui traite de la "Mise
en œuvre pratique de la méthode des différences
finies pour la cuve électrolytique perturbée", rendez-vous à
la page "MDFPOT"...
•
Grâce à la méthode des différences finies
nous accédons de manière purement numérique
à "l'expression" du potentiel électrique au sein de
l'électrolyte.
• Bien que cette
représentation soit purement intellectuelle... nous pouvons
justement
représenter par une surface, le potentiel `V(x,y)`.
• Ce qui est plus
satisfaisant, c'est que l'on peut représenter les lignes
équipotentielles au sein de l'électrolyte, et
expérimentalement c'est une mesure parfaitement
réalisable.
• Il est
délicat, voire difficile, d'intégrer des équations
aux dérivées partielles, c'est pourquoi la méthode
des différences finies peut être d'une aide
précieuse.
• Cependant, une
fois encore, nous
avons dû faire une analyse fine du système physique
proposé pour conditionner convenablement les algorithmes de
calcul, et nous avons fait "un peu de
belle
physique"...
• Cette page
n'aurait pas pu être composée sans les "outils" fournis
par AsciiMath, à l'URL
: <http://asciimath.org/>.
• Cette page a pu
être développée et affichée correctement
grâce à l'utilisation du réseau de distribution de
contenu MathJax (CDN). Toute
la documentation relative à MathJax
est accessible à l'URL :
<http://docs.mathjax.org/en/latest/index.html>.
• Les graphes et
les animations ont
été tracés à l'aide du logiciel
gnuplot®, dont la documentation est
accessible à l'URL :
<http://www.gnuplot.info/>.
Retour à la
page principale...