Étude du mouvement du pendule pesant.
Mise en œuvre de la méthode de RUNGE-KUTTA RK4,4.
1. Étude "mécanique" du pendule pesant.
1.1. Position du problème.
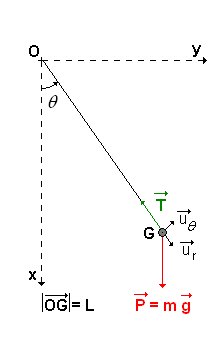• Une
masse m
est attachée par un fil inextensible de longueur L à un point O.
• La
masse m
est soumise à
l'action de la
pesanteur caractérisée par l'accélération `vec g`.
• La masse m est donc
soumise à
son poids : `color(red)(vecP =
mvecg)`.
• La masse m est également
soumise à la tension : `color(green)(vecT)` du câble qui la lie au point O.
• La masse m oscille dans
le plan (xOy), de part et d'autre de
l'axe `vec"Ox"`.
• Ce "système" mécanique, modélise un pendule pesant...
1.2. Équations de la mécanique.
• On note `veca` l'accélération prise par la masse m sous l'action des forces `vecP`et
`vecT` ; d'après la deuxième loi de NEWTON, il vient
:
`m veca = vecP + vecT`.
• On utilise les coordonnées polaires et le repère local (G, `vecu_r`,
`vecu_theta`).
• On peut écrire : `vecP=[(mgcos(theta)),(-mgsin(theta)),(0)]`,
`vecT=[(-T),(0),(0)]`et `vec"OG"=[(L),(0),(0)]`.
• La vitesse instantanée de la masse m est donnée par
:
`vecv = frac{"d"vec"OG"} {dt}` ; soit `vecv=[(0),(Lfrac{"d"theta}
{"d"t}),(0)]`.
• L'accélération de la masse m est donnée par
: `veca=[(-L(frac{"d"theta} {"d"t})^2),(Lfrac{"d"^2theta}
{"d"^2t}),(0)]`.
• Partant de : `m veca = vecP + vecT`, avec
`"m"veca=[(-"m"L(frac{"d"theta} {"d"t})^2),("m"Lfrac{"d"^2theta}
{"d"^2t}),(0)]`.
Il vient : `-mL(frac{"d"theta} {"d"t})^2 = mgcos(theta) - T`, soit encore :
`color(red)(mL(frac{"d"theta} {"d"t})^2 = T - mgcos(theta))`.
Et : `"m"Lfrac{"d"^2theta} {"d"^2t} = -mgsin(theta)`, soit
encore :
`color(navy)(frac{g}{L}frac{"d"^2theta} {"d"^2t} +sin(theta) = 0)`.
1.3. Mise en "forme" de l'équation de la mécanique.
• Suivant les usages... Nous
allons mettre l'équation sous forme canonique.
- Partant de : `frac{L}{g}frac{"d"^2theta} {"d"^2t} +sin(theta) = 0`.
- Nous écrivons : `color(navy)(frac{1}{omega_n^2}frac{"d"^2theta}
{"d"^2t}
+sin(theta) = 0)`.
Où `omega_n` désigne la pulsation naturelle du système physique (`f_n =
frac{omega_n}{2pi}`) en est la fréquence naturelle.
Ici : `frac{1}{omega_n^2} = frac{L}{g} implies omega_n =
sqrt(frac{g}{L})`.
• Précisons également les conditions initiales :
- À la date `t = t_0` (avec `t_0 = 0`) :
`theta = theta_0`.
La vitesse angulaire donnée par : `frac{d theta}{dt}` est égale à
`(frac{d theta}{dt})_(t_0) = 0`.
2. Résolution de l'équation de la mécanique.
Mise en œuvre de la méthode de RUNGE-KUTTA RK4,4.
2.1. La méthode de RUNGE-KUTTA RK4,4.
• La méthode
de
RUNGE-KUTTA RK4,4
est une méthode numérique permettant de résoudre
dans le cas le plus général, un système
d'équations différentielles ordinaires (EDO) du premier
ordre par approximation. Cette méthode a été mise
au point par les mathématiciens Carl
RUNGE et Martin Wilhelm KUTTA.
- Rappelons qu'une équation différentielle
ordinaire (EDO) de degré n, est de la forme :
`F(x,y(x),doty(x),ddoty(x),...,y^((n)) (x))=0`, où `y^((n)) (x)`
est la derivée n-ième de `y(x)` par rapport à `x`.
- Pour une équation différentielle
ordinaire du premier ordre, on calcule la solution de l'équation
différentielle par itération, le raffinement de la
méthode conduit à une erreur d'ordre quatre.
- Lorsque l'on a affaire à une
équation différentelle ordinaire d'ordre n
supérieur ou égal à deux, on peut la
décomposer en un système
de n équations
différentielles ordinaires du premier ordre. On constitue alors
un espace vectoriel des solutions, de dimension fini ; on dit que
l'équation différentielle ordinaire de degré n est une
fonction à valeur vectorielle. Bien entendu, la méthode
de RUNGE-KUTTA RK4,4
s'applique à chaque composante vectorielle.
2.2. Mise en œuvre pratique de la méthode de
RUNGE-KUTTA RK4,4.
2.2.1. Écriture du système d'équations
différentielles ordinaires du premier ordre.
• Partant de l'équation de
la mécanique :
`frac{1}{omega_n^2}frac{"d"^2theta} {"d"^2t}
+sin(theta) = 0`, on observe que cette équation différentielle du
deuxième ordre, n'est pas linéaire !
• Nous pouvons écrire
l'équation sous la forme : `frac{1}{omega_n^2}ddottheta
+sin(theta) = 0`.
- Où : `dottheta = frac{"d"theta}{"d"t}`, et où `ddottheta =
frac{"d"dottheta}{dt}`.
- On peut encore écrire : `ddot theta = -omega_n^2sin(theta)`.
• Nous allons
décomposer cette équation différentielle ordinaire
du second ordre, en un système de deux
équations
différentielles
ordinaires du premier ordre.
• Posons : `u_0 = theta`, et
`u_1 = frac{"d"u_0}{"d"t}`, on en déduit `u_1 = dottheta`, et
`frac{"d"u_1}{"d"t} = ddottheta`.
• L'équation de la mécanique
s'écrit alors : `frac{"d"u_1}{"d"t} = -omega_n^2sin(u_0)`.
• Nous devons
donc résoudre le systèmes
de deux équations
différentielles ordinaires du premier ordre suivant :
`color(navy)(frac{"d"u_0}{dt} = u_1)`.
`color(navy)(frac{"d"u_1}{"d"t} = -omega_n^2sin(u_0))`.
• Où :
`u_0 = u_0(t)` et `u_1 = u_1(t)` sont des fonctions du temps.
Remarque : On a
affaire à un système d'équations couplées.
2.2.2. Conditionnement du calcul.
• Dans la
méthode de RUNGE-KUTTA
RK4,4, on programme le système des
deux équations différentielles ordinaires du premier
ordre, et on précise les conditions initiales (ici au nombre
de deux).
• À la date `t = t_0`,
avec (`t_0 = 0`), `theta(t_0) = theta_0 implies u_0(0) = theta_0`, et
`(frac{"d"theta}{"d"t})_(t_0)= 0 implies u_1(0) = 0`.
• L'algorithme de
la méthode de RUNGE-KUTTA
RK4,4 élabore une "table de
données" constituée de n
lignes contenant chacune le
triplet : `"{"t, u_0(t),
u_1(t)"}"`.
- On résoud bien notre problème sous forme
numérique, et l'exploitation de la "table de données"
permet ici de donner l'évolution de l'élongation angulaire `theta(t)`
du pendule en fonction du temps.
3. Représentations graphiques de l'élongation angulaire du pendule.
3.1. L'élongation angulaire initiale est de 10 degrés.
3.1.1. Initialisation des calculs.
• On choisit : L =
24,82 cm avec `g approx
9,80 m.s^"-2"`, ce qui implique `omega_n approx 2pi
rd.s^(-1)`...
• Ici `t`
prend
ses
valeurs dans l'intervalle `[0, t_(Max)]`, et varie au pas `Delta t` ,
avec :
`t_(Max) = 5 s`, et `Deltat = 500`µs.
• À la date `t = 0`,
`u_0(0) = 10` degrés (en fait ces degrés seront convertis en
radians...), et `u_1(0) = 0`.
• Nous
obtiendrons une "table de données" formée de dix
mille lignes contenant chacune le
triplet : `"{"t, u_0(t), u_1(t)"}"`.
3.1.2. Évolution de θ(t).
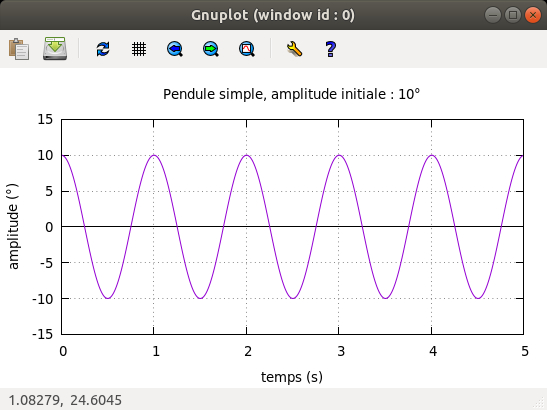
Remarque : Le graphe
a été réalisé à l'aide du logiciel gnuplot®, et à partir de la "table de données" élaborée par la
méthode RK4,4.
• Comme `omega_n
approx 2pi
rd.s^(-1)`, cela implique que la période du pendule est sensiblement
égale à 1 seconde. Et dans le cas "d'une amplitude faible à
l'état initial", on doit retrouver cette valeur, ce qui est bien
le cas ici !
3.1.3. Évolution de `bb dot theta` en fonction de `bb theta`, étude
dans le plan de phase .
Remarque : Le graphe
a été réalisé à l'aide du logiciel gnuplot®, et à partir de la "table de données" élaborée par la
méthode RK4,4.
• Pour une amplitude
initiale faible, et une vitesse initiale nulle, on montre que : `theta
= theta_0cos(omega_n t)`.
- On calcule : `v_theta = frac{"d"theta}{"d"t} implies v_theta =
dot theta`, c'est la vitesse angulaire du pendule ; `dot theta = -
omega_ntheta_0sin(omega_n t)`.
- On peut écrire : `sin^2(omega_n t) = frac{dot
theta^2}{theta_0^2omega_n^2}`, et `cos^2(omega_n t) =
frac{theta^2}{theta_0^2}`.
- Comme : `sin^2(omega_n t) + cos^2(omega_n t) = 1` ; il en résulte :
`color(navy)(frac{dot theta^2}{theta_0^2omega_n^2} +
frac{theta^2}{theta_0^2} = 1)`.
• Le graphe dans le
plan de phase de `dot theta` en fonction de `theta` est une ellipse
dont le demi
axe suivant `theta` est égal à : `color(navy)(a = theta_0)`, et
dont le demi
axe suivant `dot theta` est égal à : `color(navy)(b = theta_0
omega_n)`. C'est bien ce que nous observons !
Application numérique :
`a = theta_0 implies a = 10` (degrés) ; `b = theta_0 omega_n`,
avec `omega_n approx 2pi rd.s^(-1) implies b = 62,8` (degrés/s)...
• Ainsi, pour les
faibles amplitudes initiales, le mouvement du pendule pesant est bien
(ici) une fonction cosinusoïdale du temps de période `T = 2pi
sqrt(frac{L}{g})`.
3.2. L'élongation angulaire initiale est de 178 degrés.
3.2.1. Initialisation des calculs.
• On choisit : L =
24,82 cm avec `g approx
9,80 m.s^"-2"`, ce qui implique `omega_n approx 2pi
rd.s^(-1)`...
• Ici `t`
prend
ses
valeurs dans l'intervalle `[0, t_(Max)]`, et varie au pas `Delta t` ,
avec :
`t_(Max) = 5 s`, et `Deltat = 500`µs.
• À la date `t = 0`,
`u_0(0) = 178` degrés (en fait ces degrés seront convertis en
radians...), et `u_1(0) = 0`.
• Nous
obtiendrons une "table de données" formée de dix
mille lignes contenant chacune le
triplet : `"{"t, u_0(t), u_1(t)"}"`.
3.2.2. Évolution de θ(t).
Remarque : Le graphe
a été réalisé à l'aide du logiciel gnuplot®, et à partir de la "table de données" élaborée par la
méthode RK4,4.
• La période du
pendule est sensiblement égale à 3,5 secondes.
• Si le signal est
bien périodique, il n'est plus représenté (ici) par une fonction
cosinusoïdale du temps !
• En conclusion, on
peut affirmer que la période T du pendule
pesant dépend de l'amplitude des oscillations, elle est d'autant plus
grande que cette même amplitude est élevée.
3.2.3. Évolution de `bb dot theta` en fonction de `bb theta`, étude
dans le plan de phase .
Remarque : Le graphe
a été réalisé à l'aide du logiciel gnuplot®, et à partir de la "table de données" élaborée par la
méthode RK4,4.
• Ce graphe "fermé",
nous indique que le pendule pesant a bien un mouvement périodique, cependant
il ne peut être une fonction sinusoïdale du temps !
4. Intérêt pratique et remerciements.
4.1. Intérêt pratique.
• L'élongation angulaire du pendule pesant
vérifie, on le rappelle, l'équation différentielle du second ordre
`frac{1}{omega_n^2}frac{"d"^2theta} {"d"^2t}
+sin(theta) = 0`. Cette équation n'admet pas de solution analytique
"simple" ; aussi la méthode
de RUNGE-KUTTA RK4,4
nous facilite telle les calculs, en effet, on ne procède qu'à
des dérivations qui nous conduisent à écrire un système des
deux équations différentielles ordinaires du premier
ordre, et on procède alors à l'intégration
numérique.
4.2. Remerciements.
• J'adresse mes plus vifs
remerciements à Monsieur John
BURKARDT, Chercheur
invité du Département Informatique Scientifique, Florida State University (FSU) : John BURKARDT.
• Monsieur John
BURKARDT met à notre disposition, le code source
écrit en C, de la méthode
de RUNGE-KUTTA RK4,4,
sous le vocable rk4.c,
et un fichier d'en-tête rk4.h.
- Deux algorithmes sont
développés :
• "RK4 takes one Runge-Kutta step for a scalar ODE", qui permet de
résoudre une
équation différentielle ordinaire du premier ordre.
• "RK4VEC takes one Runge-Kutta step for a vector ODE", qui permet
de résoudre un système de n
équations différentielles ordinaires du premier ordre,
l'équation différentielle ordinaire d'ordre n à
l'origine de ce système de n
équations différentielles ordinaires du premier ordre,
est
"bien" une fonction à valeur vectorielle.
• Monsieur John
BURKARDT met également à notre disposition, le
code
source écrit en C, de deux exemples permettant de tester les
deux algorithmes proposés, sous le vocable rk4_prb.c.
- Les trois fichiers peuvent être
téléchargés à l'URL : <https://people.sc.fsu.edu/~jburkardt/c_src/rk4/rk4.html>.
• Pour ma
part, je vous
propose de consulter un document html que j'ai rédigé
à votre intention et qui traite de la "Mise en œuvre
pratique de la méthode RK4,4 ", rendez-vous à la page
"PDRK4"...
• Cette page n'aurait pas pu
être
composée sans les "outils" fournis par AsciiMath, à l'URL : <http://asciimath.org/>.
• Cette page a pu être
développée et affichée correctement grâce
à l'utilisation
du réseau de distribution de contenu MathJax (CDN). Toute la
documentation relative à MathJax
est accessible à l'URL : <http://docs.mathjax.org/en/latest/index.html>.
• Les graphes ont
été tracés à l'aide du logiciel
gnuplot®, dont
la documentation est accessible à
l'URL : <http://www.gnuplot.info/>.
Retour à la page principale...
Copyright© 2016-2019
[ DR ] Tous droits
réservés.