Équation des télégraphistes.
1. Modélisation électrique d'un élément
de longueur d'une ligne bifilaire ou d'un câble coaxial.
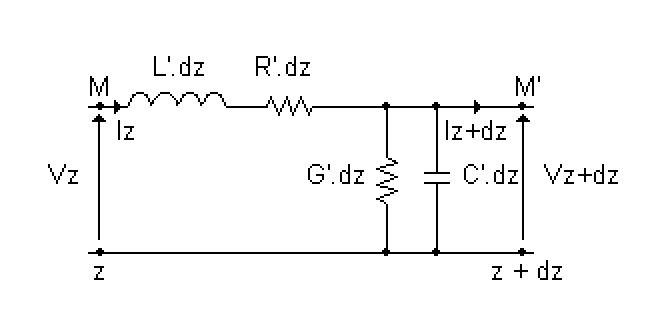
1.1. Schéma de modélisation.
•
On modélise un tronçon d'une ligne bifilaire qui
s'étend suivant l'axe des cotes z,
entre les plans de cote z et z+dz.
- L' est l'inductance linéique de la ligne (H.m-1).
- R' est la résistance linéique de la ligne (Ω.m-1).
- G' est la conductance linéique de la ligne (S.m-1).
- C' est la capacité linéique de la ligne (F.m-1).
- Vz : potentiel au point M dans le plan
de cote z.
- Iz : courant au point M dans le plan
de cote z.
- Vz+dz : potentiel au point M' dans le
plan
de cote z+dz.
- Iz+dz : courant au point M' dans le
plan
de cote z+dz.
1.2. Exemples.
1.2.1. Données relatives au câble coaxial.

•
Deux conducteurs métalliques C1 et C2 de
forme cylindrique, coaxiaux, de longueur "infinie" sont en influence
totale.
- C1 est le conducteur central, c'est un fil de cuivre.
- C2 constitue la tresse métallique,
formée de fils de cuivre entrecroisés...
•
On suppose que l’espace entre les conducteurs C1 et C2
est occupé par un isolant (diélectrique) dont la
permittivité
diélectrique relative est égale à εr.
•
On démontre que la capacité linéique
(capacité par unité de longueur) du câble coaxial
est donnée par la relation :
`C'=(2 pi epsilon_0 epsilon_r)/ln(D_2/D_1)`.
• Où : ε0 est la permittivité
diélectrique du vide, avec `epsilon_0=1/(36 pi 10^9)` F.m-1.
• Où : εr est la permittivité
diélectrique relative du diélectrique (c'est un nombre
pur).
• Où : D2 est le diamètre "occupé"
par le
conducteur central et le diélectrique.
• Où : D1 est le diamètre du conducteur
central.
•
On démontre également que l'inductance linéique
(inductance par unité de longueur) du câble coaxial
est donnée par la relation :
`L'=mu_0/(2 pi) ln(D_2/D_1)`.
• Où : μ0 est la perméabilité
magnétique du vide, avec `mu_0=4 pi 10^(-7)` H.m-1.
1.2.2. Données relatives à la ligne bifilaire.

•
Deux fils conducteurs rectilignes infiniment longs sont distants de D
. Les fils sont parallèles entre eux et à l'axe Oz ; ils
sont contenus dans le plan (Ox, Oz). Les fils ont le même
diamètre d ;
l’axe de
symétrie du fil situé à gauche de l'axe Oz passe
le point `A(-D/2,0,0)` ; l’axe de symétrie du fil
situé à droite de l'axe Oz passe par le point
`B(D/2,0,0)`. Les deux fils conducteurs sont séparés par
un isolant (diélectrique) de permittivité
diélectrique relative εr ; on suppose
que d << D.
•
On démontre que la capacité linéique
(capacité par unité de longueur) de la ligne bifilaire
est donnée par la relation :
`C'=(pi epsilon_0 epsilon_r)/ln((2D-d)/d)`.
• Où : ε0 est la permittivité
diélectrique du vide, avec `epsilon_0=1/(36 pi 10^9)` F.m-1
• Où : εr est la permittivité
diélectrique relative du diélectrique (c'est un nombre
pur).
• Où : D est la distance entre les deux fils conducteurs.
• Où : d est le diamètre de chacun des
fils conducteurs.
•
On démontre également que l'inductance linéique
(inductance par unité de longueur) de la ligne bifilaire
est donnée par la relation :
`L'=mu_0/pi ln((2D-d)/d)`.
• Où : μ0 est la perméabilité
magnétique du vide, avec `mu_0=4 pi 10^(-7)` H.m-1.
1.3. Les équations de l'électricité.
1.3.1. Appliquons la loi des branches entre les points M et M'.
•
`V_z - V_(z+dz)= L'dz(del I_z)/(del t)+R'dzI_z`.
• Soit : `-(del V_z )/(del z) dz= L'dz(del I_z)/(del
t)+R'dzI_z rArr -(del V_z )/(del z)= L'(del I_z)/(del t)+R'I_z`.
- Soit encore : `-(del V )/(del z)= L'(del I)/(del
t)+R'I`.
1.3.2. Appliquons la loi des nœuds au point M'.
•
`I_z=G'dzV_z+C'dz(del V_z)/(del t)+I_(z+dz)`.
• Soit : `-(del I_z)/(del z)dz=G'dzV_z+C'dz(del V_z)/(del t)
rArr -(del I_z)/(del z)=G'V_z+C'(del V_z)/(del t)`.
- Soit encore : `-(del I)/(del z)=C'(del V)/(del
t)+G'V`.
1.3.3. Supposons que la ligne soit sans pertes.
• Cette
hypothèse nous indique qu'il n'y a pas consommation de puissance
active, ici il s'agirait de l'effet Joule `rArr R'=0` et
`G'=0`.
• Les équations
de l'électricité s'écrivent alors :
`color (navy)(-(del V )/(del z)= L'(del I)/(del
t))`.
`color (navy)(-(del I)/(del z)=C'(del V)/(del
t))`.
2. Recherche de la solution de l'équation des
télégraphistes.
2.1. Intéressons nous au potentiel V.
• Dérivons la
relation : `-(del V )/(del z)= L'(del I)/(del
t)` par rapport à la cote z
à t = constante.
- Il vient : `-(del^2 V )/(del z^2)= L'(del^2 I)/(del z del
t)`.
• Dérivons la
relation : `-(del I)/(del z)=C'(del V)/(del
t)` par rapport au temps t
à z = constante.
- Il vient : `-(del^2 I)/(del t del z)=C'(del^2 V)/(del
t^2)`.
• Nous supposons que le
potentiel V et le courant I, vérifient la relation de SCHWARZ.
- Il vient : `(del^2 I)/(del z del
t)=(del^2 I)/(del t del z) rArr -1/(L')(del^2 V)/(del z^2)=-C'(del^2
V)/(del t^2)`.
- Soit : `color (navy)((del^2 V)/(del z^2)-L'C'(del^2 V)/(del
t^2)=0)`.
• Nous reconnaissons
une équation des ondes de la forme : `(del^2 V)/(del
z^2)-1/(c^2)(del^2 V)/(del t^2)=0`
- Ici : `1/(c^2)=L'C' rArr color (navy)(c=1/sqrt(L'C'))`.
• Le potentiel V obéit à une équation des ondes, la
célérité c
de cette onde dépend a priori des caractéristiques
électriques de la ligne ; nous venons d'établir l'équation
dite des
télégraphistes.
2.2. Intéressons nous au courant I.
• Dérivons la
relation : `-(del V )/(del z)= L'(del I)/(del
t)` par rapport au temps t
à z = constante.
- Il vient : `-(del^2 V )/(del t del z)= L'(del^2 I)/(del t^2)`.
• Dérivons la
relation : `-(del I)/(del z)=C'(del V)/(del
t)` par rapport à la cote z
à t = constante.
- Il vient : `-(del^2 I)/(del^2 z)=C'(del^2 V)/(del z del
t)`.
• En vertu de la
relation de SCHWARZ, il vient
: `(del^2 V)/(del t del
z)=(del^2 V)/(del z del t) rArr -L'(del^2 I)/(del t^2)=-1/(C')(del^2
I)/(del z^2)`.
- Soit : `color (navy)((del^2 I)/(del z^2)-L'C'(del^2 I)/(del
t^2)=0)`.
• Une nouvelle fois,
nous reconnaissons
une équation des ondes de la forme : `(del^2 I)/(del
z^2)-1/(c^2)(del^2 I)/(del t^2)=0`
- Ici : `1/(c^2)=L'C' rArr color (navy)(c=1/sqrt(L'C'))`.
• Le courant I obéit à une équation des ondes, la
célérité c
de cette onde dépend a priori des caractéristiques
électriques de la ligne.
2.3. Solution de l'équation des ondes concernant le
potentiel V.
• Partant de :
`(del^2 V)/(del z^2)-1/(c^2)(del^2 V)/(del
t^2)=0`, où `c=1/sqrt(L'C')`, nous savons que la solution de
cette équation est la combinaison linéaire de deux
fonctions.
- On écrit : `color (navy)(V(t,z)=f_1(t-z/c)+g_1(t+z/c))`.
`f_1(t-z/c)` est une onde de potentiel progressive, qui se
propage
dans le sens positif de l'axe des cotes.
`g_1(t+z/c)` est une onde de potentiel rétrograde
(ou
régressive), qui se propage dans le sens négatif de l'axe
des
cotes, cette onde est liée à la réflexion de
l'onde progressive sur un "obstacle", voire l'extrémité
de la ligne...
2.4. Solution de l'équation des ondes concernant le courant
I.
2.4.1. Observation générale.
• Partant de :
`(del^2 I)/(del z^2)-1/(c^2)(del^2 I)/(del
t^2)=0`, où `c=1/sqrt(L'C')`, nous savons que la solution de
cette équation est la combinaison linéaire de deux
fonctions.
- On écrit : `I(t,z)=f_2(t-z/c)+g_2(t+z/c)`.
`f_2(t-z/c)` est une onde de courant progressive.
`g_2(t+z/c)` est une onde de courant rétrograde (ou
régressive).
• Il est évident
que l'onde de courant I, et
l'onde de potentiel V ne sont
pas indépendantes l'une de l'autre, en effet elles sont
liées par les deux relations :
`-(del V )/(del z)= L'(del I)/(del
t)`.
`-(del I)/(del z)=C'(del V)/(del
t)`.
2.4.2. Conséquences.
• On suppose que
l'on
connaît la solution de l'onde de potentiel, soit :
`V(t,z)=f_1(t-z/c)+g_1(t+z/c)`.
• On fait le changement
de variables :
`u=t-z/c`.
`v=t+z/c`.
- Alors : `V(t,z)=f_1(u)+g_1(v)`.
- Il vient :
• `du=dt-1/cdz`.
• `dv=dt+1/cdz`.
- On pose :
• `f_1^•(u)=(df_1(u))/(du)`.
• `g_1^•(v)=(dg_1(v))/(dv)`.
• Donnons l'expression
de la différentielle de `f_1` :
`df_1=(del f_1)/(del t)dt+(del f_1)/(del z)dz`.
`df_1=f_1^•(u)(dt -1/cdz)`.
- Il vient :
• `(del f_1)/(del t)=f_1^•(u)`.
• `(del f_1)/(del z)=-1/c f_1^•(u)`.
• Donnons l'expression
de la différentielle de `g_1` :
`dg_1=(del g_1)/(del t)dt+(del g_1)/(del z)dz`.
`dg_1=g_1^•(v)(dt +1/cdz)`.
- Il vient :
• `(del g_1)/(del t)=g_1^•(v)`.
• `(del g_1)/(del z)=1/c g_1^•(v)`.
• Partant de :
`V(t,z)=f_1(u)+g_1(v)`
- On écrit :
• `dV=(del V)/(del t)dt+(del V)/(del z)dz`.
•
`dV=(f_1^•(u)+g_1^•(v))dt-1/c(f_1^•(u)-g_1^•(v))dz`.
- Il vient :
• `(del V)/(del t)=f_1^•(u)+g_1^•(v)`.
• `(del V)/(del z)=-1/c(f_1^•(u)-g_1^•(v))`.
• En prenant maintenant
en compte les deux équations électriques, on peut
écrire :
`(del I)/(del t)=-1/(L')(del V)/(del z) rArr color (navy)((del
I)/(del t)=1/(cL')(f_1^•(u)-g_1^•(v)))`.
`(del I)/(del z)=-C'(del V)/(del t) rArr color (navy)((del
I)/(del z)=-C'(f_1^•(u)+g_1^•(v)))`.
2.4.3. Intégration des équations portant sur le
courant I.
• Intégrons
l'équation : `(del
I)/(del t)=1/(cL')(f_1^•(u)-g_1^•(v))` par rapport au temps t à z
= constante.
- On écrit : `int (del
I)/(del t)dt=int 1/(cL')(f_1^•(t)-g_1^•(t))dt`
- Car ici : u = t, v = t ; il vient :
• `color (red)(I(t,z)= 1/(cL')(f_1(u)-g_1(v))`.
Remarque :
On ne
prend pas en compte l'éventuelle "constante
d'intégration" dans la mesure où initialement la ligne
est au repos (il n'y a pas d'onde de potentiel et de courant) et
où l'on cherche
l'équation d'une onde qui varie dans le temps, et dans l'espace,
ici suivant la cote z.
• Intégrons
l'équation :`(del
I)/(del z)=-C'(f_1^•(u)+g_1^•(v))` par rapport la cote z à t
= constante.
- On écrit : `int (del
I)/(del z)dz=int -C'(f_1^•(-z/c)+g_1^•(z/c))dz`
- Car ici : u = -z/c, v = z/c ; il vient :
• `color (red)(I(t,z)= cC'(f_1(u)-g_1(v))`.
• Montrons que ces deux
solutions sont identiques, aussi calculons respectivement les termes :
`1/(cL')` :
• `1/(cL')=sqrt(L'C')/(L') rArr 1/(cL')=1/sqrt((L')/(C'))`.
`cC'` :
• `cC'=(C')/sqrt(L'C') rArr cC'=1/sqrt((L')/(C'))`.
• La
quantité `sqrt((L')/(C'))` est homogène à
une résistance, c'est la résistance
caractéristique de la ligne.
- On écrit : `color (navy)(R_C=sqrt((L')/(C')))`.
• L'onde de potentiel V
s'écrit : `color (navy)(V(t,z)=f_1(t-z/c)+g_1(t+z/c))`.
• L'onde de courant I
s'écrit : `color
(navy)(I(t,z)=(f_1(t-z/c)-g_1(t+z/c))/R_C)`, avec `R_C=sqrt((L')/(C'))`.
2.5. Résumons.
• La ligne
(sans pertes) est
parcourue par une onde de potentiel V(t,z) et une
onde de courant I(t,z).
• L'onde de potentiel
se décompose en une onde progressive et une onde
rétrograde (ou régressive) ; il en est de même pour
l'onde de courant.
• L'onde de potentiel
et l'onde de courant ne sont pas indépendantes.
• On peut écrire
: `color (navy)(V(t,z)=V^(+)(t-z/c)+V^(-)(t+z/c))` ;
où `V^(+)(t-z/c)=f_1(t-z/c)` désigne l'onde de
potentiel progressive, et où `V^(-)(t+z/c)=g_1(t+z/c)`
désigne l'onde de potentiel rétrograde.
• On peut aussi
écrire : `color (navy)(I(t,z)=I^(+)(t-z/c)+I^(-)(t+z/c))`
; où `color (navy)(I^(+)(t-z/c)=(V^(+)(t-z/c))/R_C)`, et
où `color (navy)(I^(-)(t+z/c)=-(V^(-)(t+z/c))/R_C)`.
`I^(+)(t-z/c)` désigne l'onde de courant
progressive, et `I^(-)(t+z/c)` désigne l'onde de
courant rétrograde.
• Ici :
`c=1/sqrt(L'C')` désigne la célérité de
l'onde de potentiel et de l'onde de courant, c se mesure en m.s-1.
`R_C=sqrt((L')/(C'))` désigne la résistance
caractéristique de la ligne, RC se mesure en Ω.
Remarque : On a
choisi d'écrire ici : `I(t,z)=I^(+)(t-z/c)+I^(-)(t+z/c)` ;
on applique donc le théorème de superposition, les
courants doivent alors être considérés comme des
grandeurs algébriques.
2.6. Applications numériques.
2.6.1. Cas du câble coaxial.
• On donne
: Diamètre occupé par le conducteur central et le
diélectrique : D2 = 7,1 mm.
Diamètre du conducteur central : D1 = 2 mm.
Le diélectrique (isolant) est du polyéthylène de
permittivité diélectrique relative εr
= 2,3.
• On rappelle que
: `C'=(2 pi epsilon_0 epsilon_r)/ln(D_2/D_1)`.
`L'=mu_0/(2 pi) ln(D_2/D_1)`.
`epsilon_0=1/(36 pi 10^9)` F.m-1.
`mu_0=4 pi 10^(-7)` H.m-1.
• Calculons :
`c=1/sqrt(L'C')`.
`L'C'=mu_0/(2 pi) ln(D_2/D_1)(2 pi epsilon_0 epsilon_r)/ln(D_2/D_1)
rArr L'C'=mu_0 epsilon_0 epsilon_r`.
- Il vient : `c=1/sqrt(mu_0 epsilon_0 epsilon_r)`.
- Soit : `c=1/(sqrt(mu_0 epsilon_0)sqrt(epsilon_r))`.
- La quantité : `1/sqrt(mu_0 epsilon_0)` est
homogène à une vitesse, c'est la célérité
des ondes de potentiel
et de courant (on dit aussi, des ondes électromagnétiques)
quand le diélectrique est le vide, et on pose `c_0=1/sqrt(mu_0
epsilon_0)`.
- Calculons c0 :
• `1/(mu_0
epsilon_0)=(36 pi 10^9)/(4 pi 10^(-7))` m2.s-2
; `1/(mu_0
epsilon_0)=` 9.1016 m2.s-2
• c0 = 3.108 m.s-1 (300
000 km/s).
- On écrit alors : `c=c_0/sqrt(epsilon_r)`.
• Ici : `c=(3.10^8)/sqrt(2,3)` m.s-1, c =
1,978.108 m.s-1 (c
≈ 200 000 km/s).
• Calculons :
`R_C=sqrt((L')/(C'))`.
`(L')/(C')=mu_0/(2 pi) ln(D_2/D_1) ln(D_2/D_1)/(2 pi epsilon_0
epsilon_r) rArr (L')/(C')=mu_0/(4 pi^2 epsilon_0 epsilon_r)
ln^2(D_2/D_1)`.
`R_C=sqrt(mu_0/(epsilon_0)) ln(D_2/D_1)/(2 pi sqrt(epsilon_r))`.
- La quantité : `sqrt(mu_0/(epsilon_0))` est
homogène à une résistance (impédance),
c'est l'impédance d'un diélectrique constitué par
le vide (impédance du vide).
- Posons : `Z_0=sqrt(mu_0/(epsilon_0))`.
- Calculons Z0 :
• `Z_0=sqrt(4 pi 10^-7 36 pi 10^9)` Ω, Z0
= 120π Ω, soit Z0
≈ 377 Ω.
- On écrit alors : `R_C=Z_0 ln(D_2/D_1)/(2 pi
sqrt(epsilon_r))`
- Ici : `R_C=120 pi ln((7,1)/2)/(2 pi
sqrt(2,3))` Ω, RC ≈
50 Ω.
2.6.2. Cas de la ligne bifilaire.
• On donne
: Distance entre les deux fils conducteurs : D = 4 mm.
Diamètre des fils conducteurs : d = 5/10 mm.
Le diélectrique (isolant) est du polychlorure de vinyle de
permittivité diélectrique relative εr
= 3,0.
• On rappelle que
: `C'=(pi epsilon_0 epsilon_r)/ln((2D-d)/d)`.
`L'=mu_0/pi ln((2D-d)/d)`.
• Calculons :
`c=1/sqrt(L'C')`.
`L'C'=mu_0/pi ln((2D-d)/d) (pi epsilon_0 epsilon_r)/ln((2D-d)/d) rArr
L'C'=mu_0 epsilon_0 epsilon_r`.
• Comme pour le
câble coaxial, on en déduit que :
`c=c_0/sqrt(epsilon_r)`, avec c0 = 3.108 m.s-1.
`c=(3 10^8)/sqrt(3,0)` m.s-1, c
= 1,73.108 m.s-1 (c
≈ 170 000 km/s)
• Calculons :
`R_C=sqrt((L')/(C'))`.
`(L')/(C')= mu_0/pi ln((2D-d)/d) ln((2D-d)/d)/(pi epsilon_0 epsilon_r)
rArr (L')/(C')=mu_0/(pi^2 epsilon_0 epsilon_r) ln^2((2D-d)/d)`.
`R_C=sqrt(mu_0/epsilon_0) ln((2D-d)/d)/(pi sqrt(epsilon_r))`.
• Comme pour le
câble coaxial, on en déduit que : `R_C=Z_0
ln((2D-d)/d)/(pi sqrt(epsilon_r))`, avec Z0 = 120π
Ω.
`R_C=120 pi
ln((2 . 4-0,5)/(0,5))/(pi sqrt(3,0))` Ω, RC = 187,6 Ω.
3. Exemples d'illustration.
3.1. Position du problème.
• On
considère
un câble coaxial de résistance caractéristique RC,
tel que la célérité des ondes de potentiel et de
courant soit égale à c.
• La ligne a une
longueur L.
• La ligne est
alimentée par un générateur de tension qui
délivre un échelon de tension (force
électromotrice) `E = E_0.U(t)`, où `U(t)` est
l'échelon unitaire, le générateur a une
résistance interne RG.
• À son
extrémité (en z = L), la ligne charge une
résistance RL.
• On rappelle que
:
`U(t) = 0` si t < 0.
`U(t) = 1` si 0 ≤ t.

3.2. Étude des ondes
progressives de potentiel et de courant.
• Pour t < 0, on
est au repos, le potentiel et le courant sont nuls.
• Pour 0 ≤ t,
les
ondes progressives de potentiel et de courant s'installent.
• On se place à
l'entrée de la ligne, on cherche l'expression de VE =
V(t,0) et
de IE = I(t,0).
• Au début du
régime transitoire il ne peut y avoir que les ondes progressives
de tension et de courant issues du générateur.
- On peut écrire : `V(t,0) = V^(+)(t,0)`, et
`I(t,0) = I^(+)(t,0)`.
- Or : `I^(+)(t,0)
=(V^(+)(t,0))/R_C`, le générateur "voit"
une charge
égale à RC à ses bornes.
 • D'aprés la
loi
du diviseur de tension, on peut écrire :
• D'aprés la
loi
du diviseur de tension, on peut écrire :
`V^(+)(t,0)=R_C/(R_G+R_C) E_0 U(t)`.
- Soit : `V^(+)(t,0)=A E_0 U(t)`, avec
`A=R_C/(R_G+R_C)`.
• À
l'instant t,
au point M de cote z, on a : `V^(+)(t-z/c)=R_C
I^(+)(t-z/c)`, les
ondes progressives de tension et de courant, "voient" la
résistance caractéristique RC de la ligne.
• On peut alors
écrire : `color (navy)(V^(+)(t-z/c)=A E_0 U(t-z/c))`,
et `color (navy)(I^(+)(t-z/c)=(A E_0)/R_C U(t-z/c))`.
3.3. Réflexion des ondes progressives de potentiel et de
courant à l'extrémité de la ligne, naissance des
ondes rétrogrades de tension et de courant.
• Après une
durée `tau=L/c`, les ondes progressives de potentiel et de
courant atteignent l'extrémité de la ligne de longueur L,
ligne qui est "chargée"
par la résistance RL.
• À
l'extrémité de la ligne vont alors apparaître (a
priori) des ondes rétrogrades de potentiel et de courant, ces
ondes vont se superposer aux
ondes progressives.
• On peut alors
écrire à chaque instant,
en z = L :
`V(t,L)=V^(+)(t-L/c)+V^(-)(t+L/c)`, et
`I(t,L)=I^(+)(t-L/c)+I^(-)(t+L/c)`.
- Avec : `I^(+)(t-L/c)=(V^(+)(t-L/c))/R_C`, et
`I^(-)(t+L/c)=-(V^(-)(t+L/c))/R_C`.
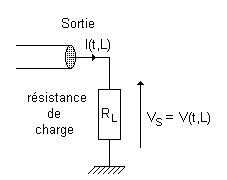 • Suivant la loi de
OHM, on peut écrire : `V(t,L)=R_L I(t,L)`.
• Suivant la loi de
OHM, on peut écrire : `V(t,L)=R_L I(t,L)`.
- Soit : `V(t,L)=R_L(I^(+)(t-L/c)+I^(-)(t+L/c))`.
- Ou bien :
`V(t,L)=R_L((V^(+)(t-L/c))/R_C-(V^(-)(t+L/c))/R_C)`.
- Soit : `V^(+)(t-L/c)+V^(-)(t+L/c)=R_L/R_C (V^(+)(t-L/c) -
V^(-)(t+L/c))`.
• Il vient :
`(R_L/R_C+1)V^(-)(t+L/c)=(R_L/R_C-1)V^(+)(t-L/c)`.
- Soit : `V^(-)(t+L/c)=(R_L-R_C)/(R_L+R_C) V^(+)(t-L/c)`.
• On pose :
`color (navy)(Gamma(L)=(R_L-R_C)/(R_L+R_C))`, c'est le coefficient de
réflexion de l'onde progressive de potentiel à
l'extrémité de la ligne.
• À
l'extrémité de la ligne l'onde de potentiel
rétrograde, est liée à l'onde de potentiel
progressive par la relation :
`color (navy)(V^(-)(t+L/c)=Gamma(L) V^(+)(t-L/c))`.
- Comme `I^(-)(t+L/c)=-(V^(-)(t+L/c))/R_C`, il vient :
• `I^(-)(t+L/c)=-Gamma(L) (V^(+)(t-L/c))/R_C`.
• Avec : `I^(+)(t-L/c)=(V^(+)(t-L/c))/R_C`,
et `color (navy)(I^(-)(t+L/c)=-Gamma(L) I^(+)(t-L/c))`.
Remarque : Si
`color (red)(Gamma(L)=0)`, alors `color (red)(V^(-)(t+L/c)=0)`,
et `color (red)(I^(-)(t+L/c)=0)`, il n'y a
pas pas d'ondes réfléchies (d'ondes
rétrogrades) de potentiel et de courant, on dit que
la "charge" est adaptée à la ligne, alors pour la
ligne sans pertes : `color (red)(R_L= R_C)`. Tout se passe alors comme
si la ligne était de longueur infinie.
3.4. Quelles sont les ondes présentes sur la ligne
pour t ∈ [ τ, 2 τ ] ?
3.4.1. Conditionnement des équations.
• On rappelle
que
`tau=L/c` est le temps mis par les ondes de potentiel et de courant
pour parcourir la ligne de longueur L.
• Considérons
uniquement l'onde de potentiel, l'onde de courant se déduisant
de l'onde de potentiel par la relation : `I(t,z)=(V^(+)(t-L/c) -
V^(-)(t+L/c))/R_C`.
• Au point M de cote z, on peut écrire :
`V^(+)(t-z/c)=A E_0 U(t-z/c)`.
• Au point M de cote z = L, on peut écrire :
`V^(-)(t+L/c)=Gamma(L) V^(+)(t-L/c)`.
Remarque : À
partir de la date origine (t - τ), avec τ ≤ t , l'onde de
potentiel rétrograde se propage du point de cote z = L au point
de cote z, en parcourant la distance (L - z) avec la
célérité c.
- On en déduit : `V^(-)(t+z/c)=A E_0 Gamma(L)
U(t-tau-(L-z)/c)`.
- Soit : `V^(-)(t+z/c)=A E_0 Gamma(L) U(t+z/c-2tau)`.
Remarque : On a bien
affaire
à une onde rétrograde car dans l'expression de
`V^(-)(t+z/c)` apparaît justement le terme `color
(red)(t+z/c)`...
- Et : `color(red)(V(t,z)=A E_0 U(t-z/c) + A E_0 Gamma(L)
U(t+z/c-2tau))`.
3.4.2. Étude de l'onde de potentiel en des points
particuliers de la ligne.
3.4.2.1. À l'extrémité de la ligne.
• Alors : z = L.
- Il vient : `V(t,L)=A E_0 U(t-tau) + A E_0 Gamma(L) U(t-tau)`,
soit `V(t,L)=A E_0 (1+ Gamma(L)) U(t-tau)`.
• On procède
à l'observation à la date τ ≤ t :
- Il vient : `V(t,L)=A E_0 (1+ Gamma(L))`.
3.4.2.2. À l'entrée de la ligne.
• Alors : z → 0+.
- Il vient : `V(t,0^(+))=A E_0 U(t) + A E_0 Gamma(L)
U(t+tau_0^(+)-2tau)`, où `tau_0^(+)=lim_(z->0^(+)) z/c`.
• On procède
à l'observation à la date t = 2τ :
- Il vient : `V(2 tau,0^(+))=A E_0 (1+ Gamma(L)) U(tau_0^(+))`,
et `V(2 tau,0^(+))=A E_0 (1+ Gamma(L))`.
Remarque : On
retrouve à l'entrée de la ligne "ce qui
se passe" à son extrémité L à la
date τ ≤ t.
3.4.2.3. Tableau donnant l'évolution de l'onde de potentiel
(méthode du tableau).

3.5. Réflexion de l'onde de potentiel rétrograde
à
l'entrée de la ligne, naissance d'une onde de potentiel
progressive "secondaire".
• Pour 2τ ≤
t,
les
ondes rétrogrades de potentiel et de courant vont
atteindre l'origine de la ligne, ligne qui est maintenant
"chargée" par la
résistance RG du
générateur (résistance de sortie du
générateur de THEVENIN
que constitue la source)...
• Ces mêmes ondes
vont donc subir une réflexion pour donner naissance à des
ondes progressives "secondaires",
si le coefficient de réflexion à l'origine Γ(0)
est différent de zéro.
- Avec : `Gamma(0)=(R_G-R_C)/(R_G+R_C)`.
• On peut écrire
ici :
`V_((2))^(+)(t-0/c)=Gamma(0)V^(-)(t+0/c)`, et
`I_((2))^(+)(t-0/c)=-Gamma(0)I^(-)(t+0/c)`.
- Où : `V_((2))^(+)(t-z/c)` est l'onde de potentiel
progressive secondaire.
- Où : `I_((2))^(+)(t-z/c)` est l'onde de courant
progressive secondaire.
Remarque : Si
`Gamma(0)=0`, alors `V_((2))^(+)(t-z/c)=0` et
`I_((2))^(+)(t-z/c)=0`, il n'y a pas d'ondes progressives "secondaires".
- Or : `Gamma(0)=(R_G-R_C)/(R_G+R_C) rArr R_G=R_C`, il y a
adaptation "d'impédance" entre la ligne et le
générateur.
• Ici :
`V_((2))^(+)(t-z/c)= A E_0 Gamma(0) Gamma(L) U(t-z/c-2tau)`.
3.6. Tableau donnant l'évolution de l'onde de potentiel
(méthode du tableau).
3.6.1. La méthode du tableau dans le cas
général.
• On suppose une
fois
encore (pour des raisons évidentes de simplification...) que le
générateur délivre une force électromotrice
en forme d'échelon : `E(t)=E_0 U(t)`.
• La ligne a une
longueur L, la
célérité des ondes
électromagnétiques y est égale à c.
• On donne :
`A=R_C/(R_G+R_C)`, `Gamma(L)=(R_L-R_C)/(R_L+R_C)`,
`Gamma(0)=(R_G-R_C)/(R_G+R_C)`, et `tau=L/c`.
• On dresse le tableau.

3.6.2. Premier exemple.
• On utilise une
ligne
de résistance caractéristique RC = 75 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• La résistance
interne du générateur de tension est égale
à RG = 50 Ω, il délivre une force
électromotice E0 = 5 V, sous la forme d'un
échelon `E=E_0 U(t)`.
• La résistance
de la charge placée à l'extrémité de la
ligne est égale à RL = 330 Ω.
• On calcule :
`tau=L/c`, soit τ = 50 ns.
A = 0,6 , Γ(0) = - 0,2 , Γ(L) = 0,6296 .
• Le tableau donne :
 • La simulation graphique donne :
• La simulation graphique donne :
 Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
• Les résultats sont identiques.
• Au final le potentiel
tant en entrée qu'en sortie doit être égal
à `V_(+oo)=R_L/(R_L+R_G) E_0`, suivant la loi du diviseur
de
tension.
- Soit : `V_(+oo)=`4,34 V.
- On observe bien que VE et VS tendent bien vers
cette limite.
3.6.3. Deuxième exemple.
• On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• La résistance
interne du générateur de tension est égale
à RG = 50 Ω, il délivre une force
électromotice E0 = 5 V, sous la forme d'un
échelon `E=E_0 U(t)`.
• La résistance
de la charge placée à l'extrémité de la
ligne est égale à RL et
`R_L->+oo` (la ligne est ouverte !).
• On calcule :
`tau=L/c`, soit τ = 50 ns.
A = 0,5 , Γ(0) = 0 , Γ(L) = 1,0 .
- Il y a
adaptation "d'impédance"
entre la ligne et le
générateur.
• Le tableau donne :
 • La simulation graphique donne :
• La simulation graphique donne :
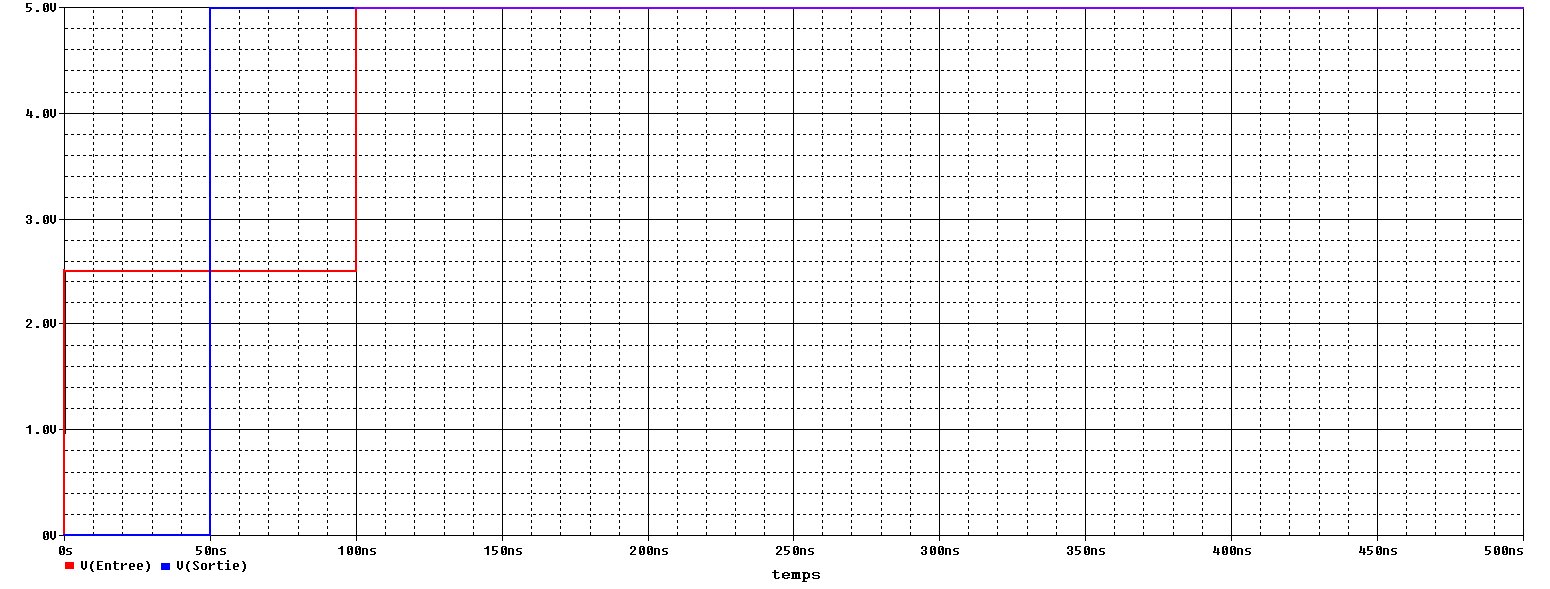 Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
• Les résultats sont identiques.
• Au final le potentiel
tant en entrée qu'en sortie doit être égal
à `V_(+oo)=E_0`, soit : `V_(+oo)=`5,0 V.
3.6.4. Troisième exemple.
• On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• La résistance
interne du générateur de tension est égale
à RG = 50 Ω, il délivre une force
électromotice E0 = 5 V, sous la forme d'un
échelon `E=E_0 U(t)`.
• La résistance
de la charge placée à l'extrémité de la
ligne est égale à RL, et RL
= 0 (la ligne est en court-circuit !) .
• On calcule :
`tau=L/c`, soit τ = 50 ns.
A = 0,5 , Γ(0) = 0 , Γ(L) = -1,0 .
- Il y a
adaptation "d'impédance"
entre la ligne et le
générateur.
• Le tableau donne :
 • La simulation graphique donne :
• La simulation graphique donne :
 Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
• Les résultats sont identiques.
• Au final le potentiel
tant en entrée qu'en sortie doit être égal
à `V_(+oo)=0` V, le court-circuit est ramené
à
l'entrée de la ligne...
Remarque : Ici la
mesure
de la duré TC du "créneau" de potentiel
à
l'entrée de la ligne permet, si l'on connaît la
célérité c
des ondes
électromagnétiques sur la ligne, de déterminer
la
longueur L de cette même
ligne, par la relation
: `L=(cT_C)/2`.
4. Étude d'un quatrième exemple où la
charge est "complexe"...
4.1. Le montage proposé, et ses propriétés.
• On
considère
un câble coaxial de résistance caractéristique RC,
tel que la célérité des ondes de potentiel et de
courant soit égale à c.
• La ligne a une
longueur L.
• La ligne est
alimentée par un générateur de tension qui
délivre un échelon de tension (force
électromotrice) `E = E_0.U(t)`, où `U(t)` est
l'échelon unitaire, le générateur a une
résistance interne RG.
• À son
extrémité (en z = L), la ligne alimente une
charge "complexe"
constituée par la mise en parallèle d'une
résistance RL, et d'une capacité CL.
• On rappelle que :
`U(t) = 0` si t < 0.
`U(t) = 1` si 0 ≤ t.
 • On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• La résistance
interne du générateur de tension est égale
à RG = 50 Ω, il délivre une force
électromotice E0 = 5 V, sous la forme d'un
échelon `E=E_0 U(t)`.
• La charge "complexe" et
constituée d'une résistance RL telle que RL
= 82 Ω, en parallèle avec un condensateur CL de
capacité égale à CL = 1,8 nF.
Remarque
: Il y a
adaptation "d'impédance"
entre la ligne et le
générateur.
4.2. Étude des ondes progressives de potentiel et de courant.
• Pour t < 0, on
est au repos, le potentiel et le courant sont nuls.
• Pour 0 ≤ t,
les
ondes progressives de potentiel et de courant s'installent.
• On se place à
l'entrée de la ligne, on cherche l'expression de VE =
V(t,0) et
de IE = I(t,0).
• Au début du
régime transitoire il ne peut y avoir que les ondes progressives
de tension et de courant issues du générateur.
- On peut écrire : `V(t,0) = V^(+)(t,0)`, et
`I(t,0) = I^(+)(t,0)`.
- Or : `I^(+)(t,0)
=(V^(+)(t,0))/R_C`, le générateur "voit"
une charge
égale à RC à ses bornes.
 • D'aprés la
loi
du diviseur de tension, on peut écrire :
• D'aprés la
loi
du diviseur de tension, on peut écrire :
`V^(+)(t,0)=R_C/(R_G+R_C) E_0 U(t)`.
- Soit : `V^(+)(t,0)=A E_0 U(t)`, avec
`A=R_C/(R_G+R_C)`.
• À
l'instant t,
au point M de cote z, on a : `V^(+)(t-z/c)=R_C
I^(+)(t-z/c)`, les
ondes pogressives de tension et de courant, "voient" la
résistance caractéristique RC de la ligne.
• On peut alors
écrire : `V^(+)(t-z/c)=A E_0 U(t-z/c)`, et
`I^(+)(t-z/c)=(A E_0)/R_C U(t-z/c)`.
• Ici : `R_G=R_C
rArr A=` 0,5.
4.3. Réflexion des ondes progressives de potentiel et de
courant à l'extrémité de la ligne, naissance des
ondes rétrogrades de tension et de courant.
4.3.1. Évolution temporelle du potentiel à
l'extrémité de la ligne.
• Après une
durée `tau=L/c`, les ondes progressives de potentiel et de
courant atteignent l'extrémité de la ligne de longueur L,
ligne qui est connectée à la charge "complexe".
• À
l'extrémité de la ligne vont alors apparaître des
ondes rétrogrades de potentiel et de courant, ces
ondes vont se superposer aux
ondes progressives.
• On peut alors
écrire à chaque instant,
en z = L :
`V(t,L)=V^(+)(t-L/c)+V^(-)(t+L/c)`, et
`I(t,L)=I^(+)(t-L/c)+I^(-)(t+L/c)`.
- Avec : `I^(+)(t-L/c)=(V^(+)(t-L/c))/R_C`, et
`I^(-)(t+L/c)=-(V^(-)(t+L/c))/R_C`.
- Et : `V^(+)(t-L/c)=A E_0 U(t-L/c)`, avec τ ≤ t
`rArr V^(+)(t-L/c)=A E_0`, alors
`color (red)(V^(+)(t-L/c))` est constant
!
 • Suivant la loi des branches on peut écrire :
• Suivant la loi des branches on peut écrire :
`V_S = V(t,L)`, soit `V(t,L)=V^(+)(t-L/c) + V^(-)(t+L/c)`.
• Suivant la loi des
noeuds on peut écrire :
`I(t,L) = I_(R_(L)) (t)+ I_(R_(L))(t)`, soit `1/R_C (V^(+)(t-L/c)
- V^(-)(t+L/c))=I_(R_(L))(t) + I_(R_(L))(t)`.
• Conséquences :
- D'après la loi de OHM
: `I_(R_L)(t)=1/R_L(V^(+)(t-L/c) + V^(-)(t+L/c))`.
- Courant de charge du condensateur :
`I_(C_L)(t)=C_L(d(V^(+)(t-L/c) + V^(-)(t+L/c)))/(dt)`.
• Soit : `I_(C_L)(t)=C_L(d(V^(+)(t-L/c)))/(dt)+
C_L(d(V^(-)(t+L/c)))/(dt)`
• Or : τ ≤ t, alors : `V^(+)(t-L/c)` est constant `rArr
I_(C_L)(t)=C_L(d(V^(-)(t+L/c)))/(dt)`.
- La loi des noeuds nous conduit à écrire :
• `1/R_C (V^(+)(t-L/c) - V^(-)(t+L/c))=1/R_L(V^(+)(t-L/c) +
V^(-)(t+L/c))+C_L(d(V^(-)(t+L/c)))/(dt)`.
• Il vient : `(R_L R_C C_L)/(R_L+R_C)
(d(V^(-)(t+L/c)))/(dt)+V^(-)(t+L/c)=(R_L-R_C)/(R_L+R_C)V^(+)(t-L/c)`.
- Pour : τ ≤ t, `V^(+)(t-L/c)=A E_0`, il vient :
`color (navy)(tau_L (d(V^(-)(t+L/c)))/(dt)+V^(-)(t+L/c)=AE_0Gamma(L))`.
• Où : `A=R_C/(R_G+R_C)`,
`Gamma(L)=(R_L-R_C)/(R_L+R_C)`, `tau_L=(R_L R_C C_L)/(R_L+R_C)`.
`tau_L` désigne la constante de temps de charge du condensateur
de capacité CL.
4.3.2. Intégrons l'équation différentielle.
• Cherchons la
solution
générale :
- Cela revient à résoudre l'équation sans second
membre, soit : `tau_L (d(V^(-)(t+L/c)))/(dt)+V^(-)(t+L/c)=0`.
- Il vient : `V^(-)(t+L/c)=C_0 e^((t-tau)/tau_L)`, ou C0
est une constante (la date origine doit être prise à (t -
τ))...
• Cherchons une
solution particulière :
- Lorsque le régime transitoire est terminé, on doit
verifier : `V^(-)(t+L/c)=AE_0Gamma(L)`.
• La solution
complète est donnée par : `V^(-)(t+L/c)=C_0
e^((t-tau)/tau_L)+AE_0Gamma(L)`.
• Condition initiale :
- À t = τ, `V^(+)(tau-L/c)+V^(-)(tau+L/c)=0` (le
condensateur n'est pas
chargé), il vient :
• `V^(-)(tau+L/c)=-V^(+)(tau-L/c)`, soit
`V^(-)(tau+L/c)=-AE_0`.
- On doit résoudre :
• `C_0+AE_0Gamma(L)=-AE_0 rArr C_0=-AE_0(1+Gamma(L))`.
• Il vient enfin
: `color
(navy)(V^(-)(t+L/c)=AE_0(Gamma(L)-(1+Gamma(L))e^(-(t-tau)/tau_L)))`.
4.3.3. Expression du potentiel à l'extémité de
la ligne.
•
`V(t,L)=V^(+)(t-L/c) + V^(-)(t+L/c)`
- Avec pour τ ≤ t : `V^(+)(t-L/c)=AE_0`, et
`V^(-)(t+L/c)=AE_0(Gamma(L)-(1+Gamma(L))e^(-(t-tau)/tau_L))`.
- Il vient pour τ ≤ t :
`color (navy)(V(t,L)=AE_0(1+Gamma(L))(1-e^(-(t-tau)/tau_L)))`.
4.3.4. Expression de l'onde de potentiel rétrograde.
• On cherche
l'expression de `V^(-)(t+z/c)` :
- Au point M de cote z, on peut écrire :
• `V^(+)(t-z/c)=A E_0 U(t-z/c)`.
- Au point M de cote z = L, on peut écrire :
•
`V^(-)(t+L/c)=AE_0(Gamma(L)-(1+Gamma(L))e^(-(t-tau)/tau_L)) U(t-tau)`.
Remarque : À
partir de la date origine (t - τ) avec τ ≤ t , l'onde de
potentiel rétrograde se propage du point de cote z = L au point
de cote z, en parcourant la distance (L - z) avec la
célérité c.
- On en déduit :
`V^(-)(t+z/c)=AE_0(Gamma(L)-(1+Gamma(L))e^(-(t-tau-(L-z)/c)/tau_L))
U(t-tau-(L-z)/c)`.
• Soit :
`V^(-)(t+z/c)=AE_0(Gamma(L)-(1+Gamma(L))e^(-(t+z/c-2tau)/tau_L))
U(t+z/c-2tau)`.
Remarque : On a bien
affaire
à une onde rétrograde car dans l'expression de
`V^(-)(t+z/c)` apparaît justement le terme `color
(red)(t+z/c)`...
- Il vient également : `color(red)(V(t,z)=A E_0 U(t-z/c) +
AE_0(Gamma(L)-(1+Gamma(L))e^(-(t+z/c-2tau)/tau_L)) U(t+z/c-2tau))`.
4.4. Étude de l'onde de potentiel en des points
particuliers de la ligne.
4.4.1. Onde de potentiel à l'extrémité de la
ligne.
• Alors z = L.
- Il vient : `V(t,L)=AE_0(1+Gamma(L))(1-e^(-(t-tau)/tau_L))
U(t-tau)`.
• Pour 0 ≤ t <
τ :
`V(t,L)=0`.
• Pour t = τ :
`V(tau,L)=0`, le condensateur agit comme un véritable
court-circuit car il n'est pas chargé !
• Pour τ < t :
`V(t,L)=AE_0(1+Gamma(L))(1-e^(-(t-tau)/tau_L))`.
- Le potentiel V(t,L) croît de manière exponentielle avec
la constante de temps τL.
• Pour t →
+∞ :
`V(+oo,L)=AE_0(1+Gamma(L))`.
`V(+oo,L)=R_C/(R_C+R_G)(1+(R_L-R_C)/(R_L+R_C)) E_0`.
`V(+oo,L)=(2R_C R_L)/((R_C+R_G)(R_L+R_C)) E_0`.
- Or `R_C=R_G rArr V(+oo,L)=R_L/(R_L+R_G) E_0`.
- Au final le potentiel en sortie doit être égal
à : `V_(+oo)=R_L/(R_L+R_G) E_0`, suivant la loi du
diviseur
de
tension.
4.4.2. Onde de potentiel à l'entrée de la ligne.
• Alors z = 0.
- Il vient : `V(t,0)=A E_0 U(t) +
AE_0(Gamma(L)-(1+Gamma(L))e^(-(t-2tau)/tau_L)) U(t-2tau)`.
• Pour 0 ≤ t
< 2τ :
`V(t,0)=A E_0`.
• Pour t = 2τ :
`V(2tau,0)=A E_0 +
AE_0(Gamma(L)-(1+Gamma(L)) rArr V(2tau,0)=0`.
• Pour 2τ < t :
`V(t,0)=A E_0 (1+Gamma(L)) (1-e^(-(t-2tau)/tau_L))`.
- Le potentiel V(t,0) croît de manière exponentielle avec
la constante de temps τL.
• Pour t →
+∞ :
`V(+oo,0)=AE_0(1+Gamma(L))`.
`V(+oo,0)=R_L/(R_L+R_G) E_0`.
- Au final le potentiel en entrée doit être égal
à : `V_(+oo)=R_L/(R_L+R_G) E_0`, suivant la loi du
diviseur
de tension.
4.4.3. Application numérique :
• Calculons :
`tau_L=(R_L R_C C_L)/(R_L+R_C)`, τL ≈ 56 ns.
• Calculons :
`V_(+oo)=R_L/(R_L+R_G) E_0`, V+∞ = 3,10 V.
4.4.4. Simulation graphique.
 Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
Remarque :
Simulation réalisée avec PSpice
Student Version release
9.1®.
• Les
prévisions
théoriques et la simulation graphique concordent.
4.4.5. Animation graphique.
• Regarder
l'animation
relative à l'évolution de l'onde de potentiel sur
la ligne, dans le
temps et dans l'espace...
5. Intérêt pratique et remerciements.
5.1. Intérêt pratique.
•
Lors de l'étude des équations aux dérivées
partielles du second ordre, nous avions dit que les
problèmes rencontrés en physique et répondant
à de telles équations, demandent la recherche
de solutions satisfaisant à des conditions particulières,
comme les conditions initiales, les conditions aux limites, ces
conditions
permettent alors de préciser de manière plus "fine"
l'expression de la solution.
•
L'étude de l'équation des télégraphistes
nous a permis d'illustrer pleinement comment mener la recherche de ces
mêmes solutions à partir de quelques exemples, et de
faire,une fois encore, "un peu de belle physique"...
5.2. Remerciements.
• Cette page
n'aurait pas pu être composée sans les "outils" fournis
par AsciiMath, à l'URL
: <http://asciimath.org/>.
• Cette page a pu
être développée et affichée correctement
grâce à l'utilisation du réseau de distribution de
contenu MathJax (CDN). Toute
la documentation relative à MathJax
est accessible à l'URL :
<http://docs.mathjax.org/en/latest/index.html>.
• Les graphes ont
été tracés à l'aide du logiciel PSpice
Student Version release
9.1®. La
documentation relative à PSpice
Student est
accessible à l'URL : <https://www.orcad.com/academic-program>.
Remarque : La
version PSpice
Student Version release
9.1® est ancienne, on peut la
télécharger à l'URL : <http://www.electronics-lab.com/downloads/circutedesignsimulation/?page=5>.
• L'animation a
été réalisée à l'aide du logiciel
gnuplot®, dont la documentation est
accessible à l'URL :
<http://www.gnuplot.info/>
Retour à la
page principale...
Copyright© 2016-2017
[ DR ] Tous droits
réservés.




 • D'aprés la
loi
du diviseur de tension, on peut écrire :
• D'aprés la
loi
du diviseur de tension, on peut écrire :  • Suivant la loi de
OHM, on peut écrire : `V(t,L)=R_L I(t,L)`.
• Suivant la loi de
OHM, on peut écrire : `V(t,L)=R_L I(t,L)`.

 • La simulation graphique donne :
• La simulation graphique donne :
 • La simulation graphique donne :
• La simulation graphique donne :
 • La simulation graphique donne :
• La simulation graphique donne :
 • On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1.
• On utilise une
ligne
de résistance caractéristique RC = 50 Ω,
de longueur
L = 10 m, la célérité des ondes
électromagnétiques est égale à c = 2.108
m.s-1. • Suivant la loi des branches on peut écrire :
• Suivant la loi des branches on peut écrire : 